Finding the shortest path – A * pathfinding
What's on this page
1. Finding the shortest path - A * pathfinding
Two months ago I posted some interesting stuff I found: Shortest path. Let me explain, someone created a workbook that calculated the shortest path between a start cell and an end cell in a maze, and it did that using only formulas. Pretty amazing. The formulas were made from Dijkstra's Algorithm. I tried to create a larger maze but the workbook grew too large.
I then found the A * pathfinding algorithm and it is a lot easier for the computer to calculate. There is a great explanation of the A * pathfinding algorithm here: Introduction to A* Pathfinding.
Basically, there is an open list, a closed list and a final path. The open list contains cells that are being considered to find the final path. The closed list contains cells that we don't need to consider again.
They all contain coordinates or cells based on criteria. The criteria are:
- The distance to the END cell. (The distance to the END cell is calculated with the Manhattan distance method.
- The distance traveled from the start cell.
If the END cell is added to the open list, the closed list is finished calculating. Now it is time to find the final path. The final path is also found using the Manhattan distance method but it can only travel on cells in the closed list.
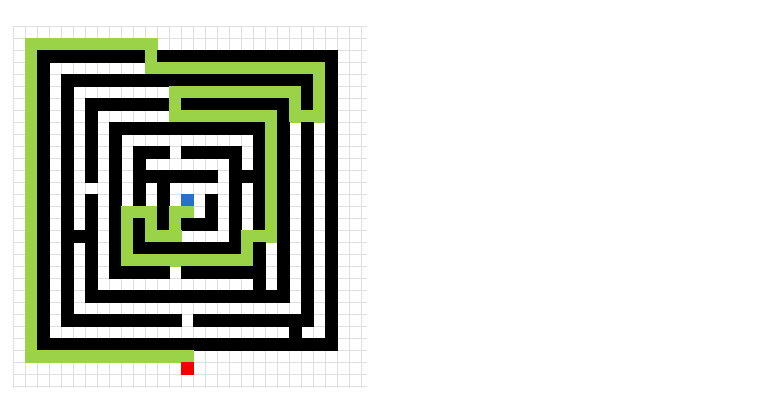
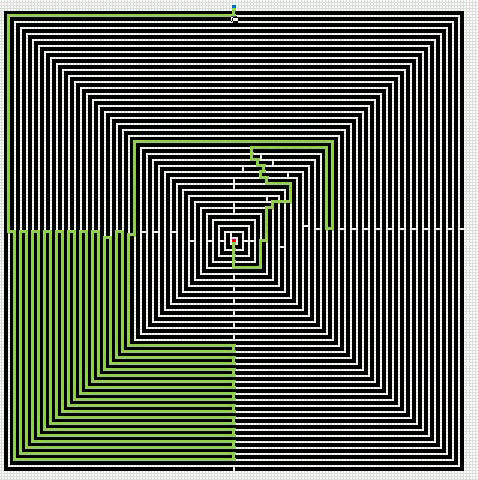
Here is an animated picture, it shows you how the macro works, simplified.
- The blue cell is the start cell
- The red cell is the end cell
- Gray cells are cells in the closed list.
- Green cells are the final path.
- Black cells are walls.
Here is a slightly more advanced "map".
This is a maze. I have removed the closed list cells to make the macro quicker.
VBA Code
'Name macro
Sub FindShortestPath1()
'Disable screen refresh
Application.ScreenUpdating = False
'Dimension variables and their data types
Dim G() As Variant
Dim H() As Variant
Dim N() As Variant
Dim OL() As Variant
Dim CL() As Variant
Dim S() As Variant
Dim E() As Variant
Dim W() As Variant
Dim Gv() As Variant
Dim i As Single
'Redimension variables
ReDim S(0 To 1)
ReDim E(0 To 1)
ReDim W(0 To 3, 0 To 1)
ReDim OL(0 To 1, 0)
ReDim CL(0 To 1, 0)
ReDim Gv(0 To 3)
'Save values in cell range specified in named range "Area" to variable Rng
Rng = Range("Area").Value
'Save the upper limit of rows from Rng variable to variable a
a = UBound(Rng, 1) - 1
'Save the upper limit of columns from Rng variable to variable a
b = UBound(Rng, 2) - 1
'Redimension variables G, H and N based on variable a and b
ReDim G(0 To a, 0 To b)
ReDim H(0 To a, 0 To b)
ReDim N(0 To a, 0 To b)
'For ... next loop from 1 to the number of rows in Rng variable
For R = 1 To UBound(Rng, 1)
'For ... next loop from 1 to the number of columns in Rng variable
For C = 1 To UBound(Rng, 2)
'Check if cell Rng(r, C) is equal to "S" (start point)
If Rng(R, C) = "S" Then
'Save number in variable R - 1 to variable S position 0 (zero)
S(0) = R - 1
'Save number in variable C - 1 to variable S position 1
S(1) = C - 1
End If
'Check if cell Rng(r, C) is equal to "E" (end point)
If Rng(R, C) = "E" Then
E(0) = R - 1
E(1) = C - 1
End If
'Check if S(0) is not equal to "" and E(0) is not equal to ""
If S(0) <> "" And E(0) <> "" Then Exit For
Next C
Next R
'Save number stored in S(0) to array variable CL (closed list) position 0,0
CL(0, 0) = S(0) 'row
'Save number stored in S(1) to array variable CL (closed list) position 1,0
CL(1, 0) = S(1) 'column
'Save -1 to array variable W position 0,0
W(0, 0) = -1
'Save 1 to array variable W position 1,0
W(1, 0) = 1
'Save 0 to array variable W position 2,0
W(2, 0) = 0
'Save 0 to array variable W position 3,0
W(3, 0) = 0
'Save 0 to array variable W position 0,1
W(0, 1) = 0
'Save 0 to array variable W position 1,1
W(1, 1) = 0
'Save -1 to array variable W position 2,1
W(2, 1) = -1
'Save 1 to array variable W position 3,1
W(3, 1) = 1
'Save boolean value False to variable Echk
Echk = False
'Keep iterating until Echk is True
Do Until Echk = True
'For ... next statement
For i = 0 To UBound(CL, 2)
'For ... next statement
For j = 0 To 3
'Save boolean value False to variable Echk
chk = False
'Add number in CL position 0, i and W position j, 0 and save total to tr
tr = CL(0, i) + W(j, 0)
'Add number in CL and W and save total to tc
tc = CL(1, i) + W(j, 1)
If tr < 0 Or tc < 0 Or tr > UBound(Rng, 1) Or tc > UBound(Rng, 2) Then
chk = True
Else
For k = UBound(CL, 2) To 0 Step -1
If tr = CL(0, k) And tc = CL(1, k) Then
chk = True
Exit For
End If
Next k
If Rng(tr + 1, tc + 1) = 1 Then chk = True
For k = UBound(OL, 2) To 0 Step -1
If tr = OL(0, k) And tc = OL(1, k) Then
chk = True
If G(CL(0, i), CL(1, i)) + 1 < G(tr, tc) Then
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
N(tr, tc) = G(tr, tc) + H(tr, tc)
End If
Exit For
End If
Next k
If chk = False Then
OL(0, UBound(OL, 2)) = tr
OL(1, UBound(OL, 2)) = tc
ReDim Preserve OL(UBound(OL, 1), UBound(OL, 2) + 1)
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
N(tr, tc) = G(tr, tc) + H(tr, tc)
If Rng(tr + 1, tc + 1) = "E" Then Echk = True
End If
End If
Next j
Next i
If Echk <> True Then
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(0, i) <> "" Then
Nchk = N(OL(0, i), OL(1, i))
Exit For
End If
Next i
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(1, i) <> "" Then
If N(OL(0, i), OL(1, i)) < Nchk And N(OL(0, i), OL(1, i)) <> "" Then
Nchk = N(OL(0, i), OL(1, i))
End If
End If
Next i
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(0, i) <> "" Then
If N(OL(0, i), OL(1, i)) = Nchk Then
ReDim Preserve CL(UBound(CL, 1), UBound(CL, 2) + 1)
CL(0, UBound(CL, 2)) = OL(0, i)
OL(0, i) = ""
CL(1, UBound(CL, 2)) = OL(1, i)
OL(1, i) = ""
End If
End If
Next i
End If
Loop
tr = E(0)
tc = E(1)
Schk = False
Do Until Schk = True
For i = UBound(CL, 2) To 0 Step -1
If CL(0, i) = (tr + 1) And CL(1, i) = tc _
And (Rng(tr + 2, tc + 1) <> "W" _
And Rng(tr + 2, tc + 1) <> "1") _
Then Gv(0) = G(tr + 1, tc)
If CL(0, i) = tr And CL(1, i) = (tc + 1) _
And (Rng(tr + 1, tc + 2) <> "W" _
And Rng(tr + 1, tc + 2) <> "1") _
Then Gv(1) = G(tr, tc + 1)
If CL(0, i) = (tr - 1) And CL(1, i) = tc _
And (Rng(tr, tc + 1) <> "W" _
And Rng(tr, tc + 1) <> "1") _
Then Gv(2) = G(tr - 1, tc)
If CL(0, i) = tr And CL(1, i) = (tc - 1) _
And (Rng(tr + 1, tc) <> "W" _
And Rng(tr + 1, tc) <> "1") _
Then Gv(3) = G(tr, tc - 1)
For j = 0 To 3
If Gv(j) <> "" Then Nf = Gv(j)
Next j
For j = 0 To 3
If Gv(j) < Nf And Gv(j) <> "" Then Nf = Gv(j)
Next j
Next i
Application.ScreenUpdating = True
Select Case Nf
Case Gv(0)
tr = tr + 1
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
Case Gv(1)
tc = tc + 1
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
Case Gv(2)
tr = tr - 1
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
Case Gv(3)
tc = tc - 1
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
End Select
If Rng(tr + 2, tc + 1) = "S" _
Or Rng(tr + 1, tc + 2) = "S" _
Or Rng(tr, tc + 1) = "S" _
Or Rng(tr + 1, tc) = "S" Then Schk = True
Loop
Application.ScreenUpdating = True
End Sub
2. Optimize pick path in a warehouse
As you probably already are aware of I have shown you earlier a vba macro I made that finds the shortest path between two points. There are obstacles between these two points to make it more difficult.

The problem with that macro is that it could only show a path that moves up, down, left or right. So I had to change it so it can move in eight directions.
Instead of using 6 movements it now uses 3 movements, it can now go diagonal from A to B. This is more realistic, of course.
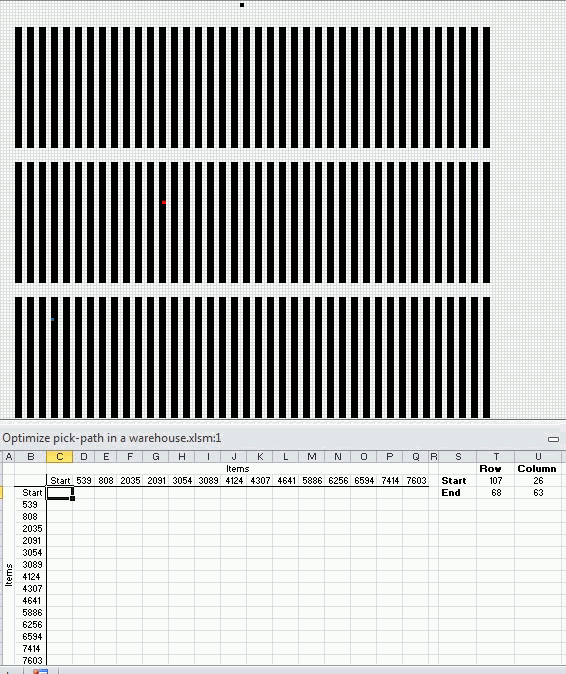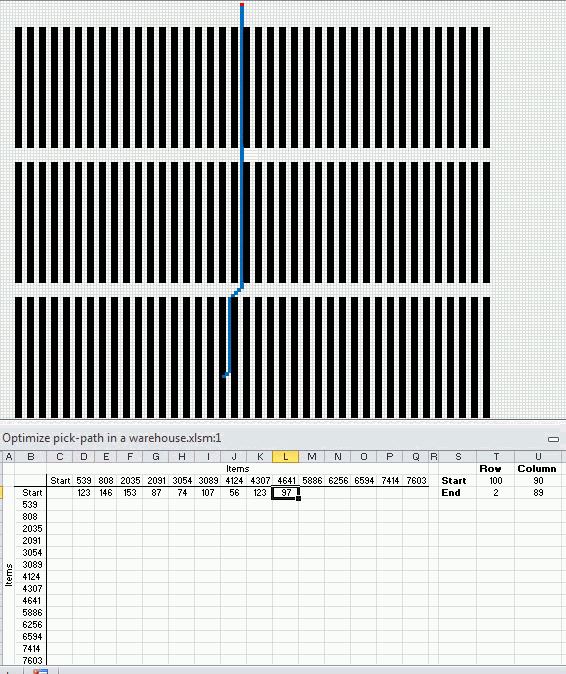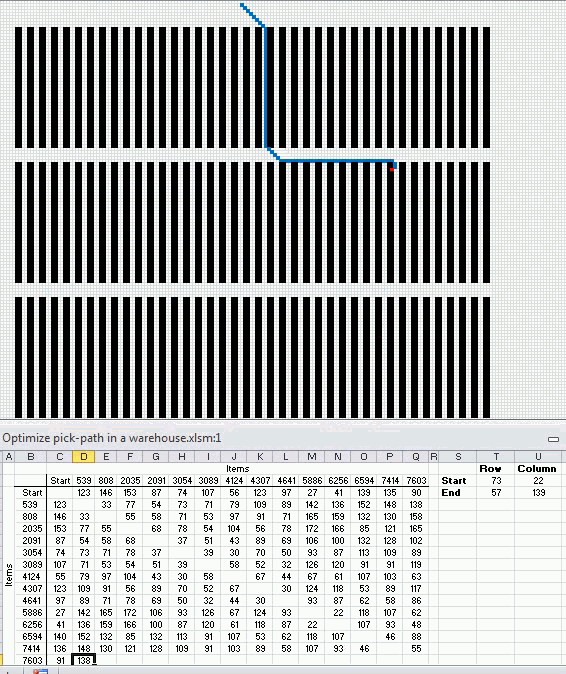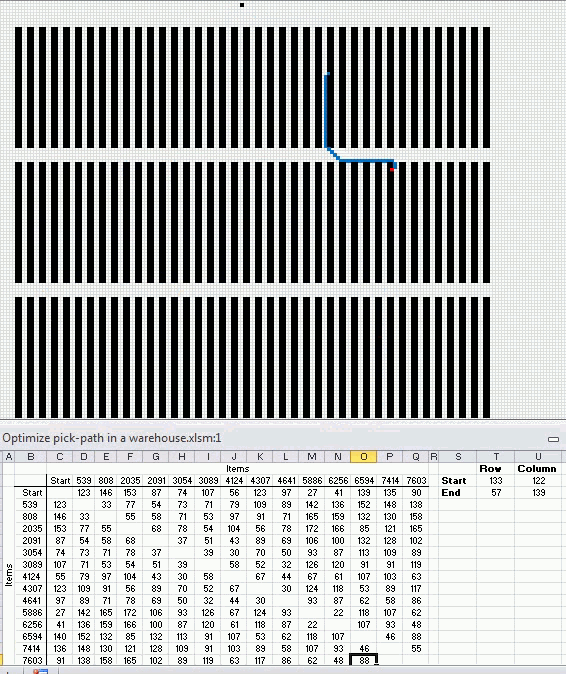
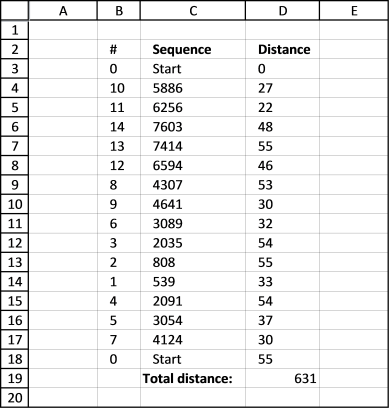
Calculating all possible paths between 15 locations
The following animated picture shows you 9600 storage locations, named item 1 to 9600. Each black dot is a storage location in this warehouse.
There is a start point almost at the top of this picture. I have chosen 14 random locations and the macro shows the shortest path and calculates the distance in the table at the bottom of this picture.
Find the shortest pick path
Now that we have all distances between 15 locations we can use the Excel Solver to find the shortest path. First we need to setup a sheet.
Formula in cell C4:
=INDEX(Items!$H$4:$H$17, MATCH('Optimize total path'!B4, Items!$G$4:$G$17, 0))
Formula in cell D4:
=INDEX(Paths!$C$3:$Q$17, MATCH('Optimize total path'!C3, Paths!$B$3:$B$17, 0), MATCH('Optimize total path'!C4, Paths!$C$2:$Q$2, 0))
Formula in cell D19:
=SUM(D3:D18)
Now it is time for the excel solver to find the optimal path. If you need more detailed instructions, check out this page: Travelling Salesman Problem in Excel Solver
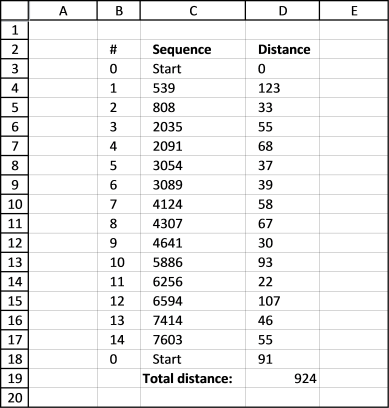
After a few minutes this sequence is shown with the shortest total distance.
Optimal path
Here is the shortest path. It begins with the start point almost at the top and goes through all 14 storage locations and then back to start point.
Read more interesting posts:
- A quicker A * pathfinding algorithm
- Finding the shortest path – A * pathfinding
- Build a maze
- Solve a maze
- Identify numbers in sum using solver
- Excel udf: Find numbers in sum
Get excel *.xlsm file
Optimize-pick-path-in-a-warehouse1.xlsm
For next statement category
The macro demonstrated above creates hyperlinks to all worksheets in the current worksheet. You will then be able to quickly […]
Table of Contents FOR NEXT statement FOR NEXT with a counter variable FOR each NEXT example FOR NEXT with counter […]
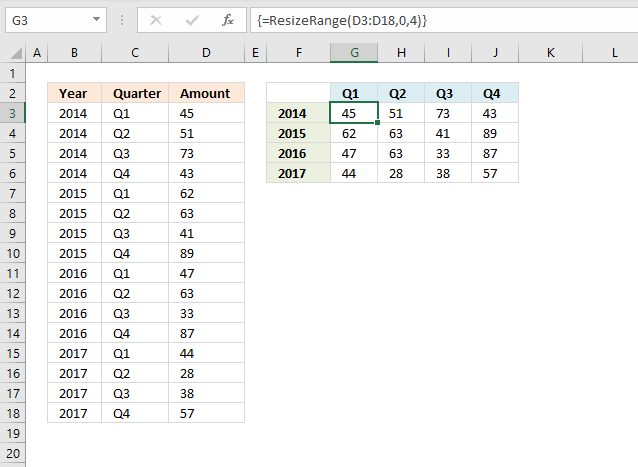
The User Defined Function (UDF) demonstrated in this article, resizes a given range to columns or rows you specify. This […]
Pathfinding category
3 weeks ago I showed you a A* pathfinding algorithm. It was extremely slow and sluggish and I have now made it […]
Excel categories
5 Responses to “Finding the shortest path – A * pathfinding”
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
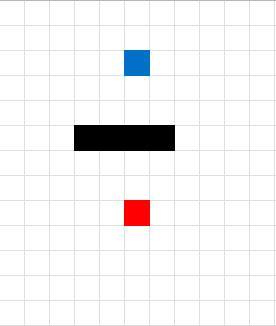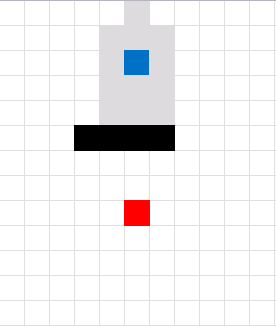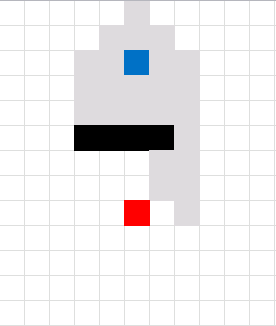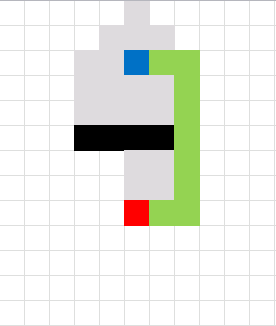



[…] I guess this is a task for vba but that will be another post. [UPDATE] The follow up post is here: Finding the shortest path – A * pathfinding […]
impressive!
Torstein,
Thank you but the idea is not mine. The A * algorithm is used in many computer games.
It is a very interesting technique and I believe I can make my macro run a lot quicker with some minor changes.
[UPDATE]
A quicker A * pathfinding algorithm
[…] Finding the shortest path – A * pathfinding […]
Nice explanation :) Here are some other visualizations with extra info, helping to better understand A* (along with forkeable examples): https://thewalnut.io/visualizer/visualize/7/6/