A quicker A * pathfinding algorithm
3 weeks ago I showed you a A* pathfinding algorithm. It was extremely slow and sluggish and I have now made it smaller and faster, much faster.
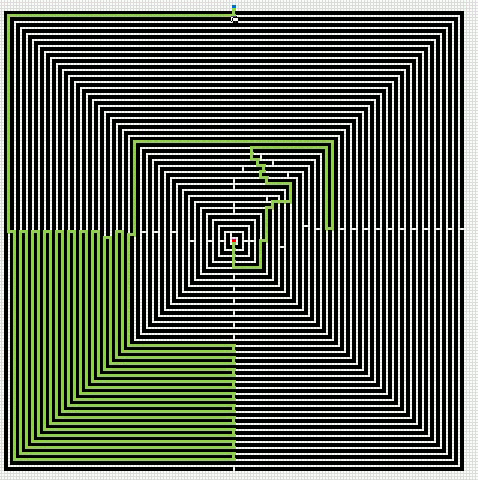
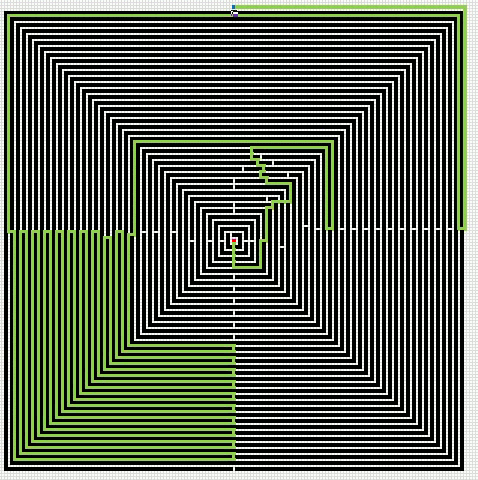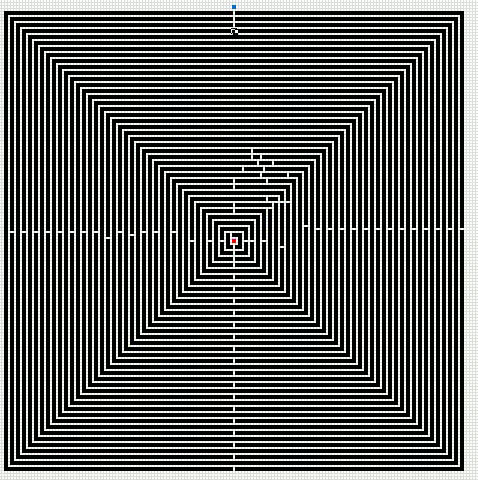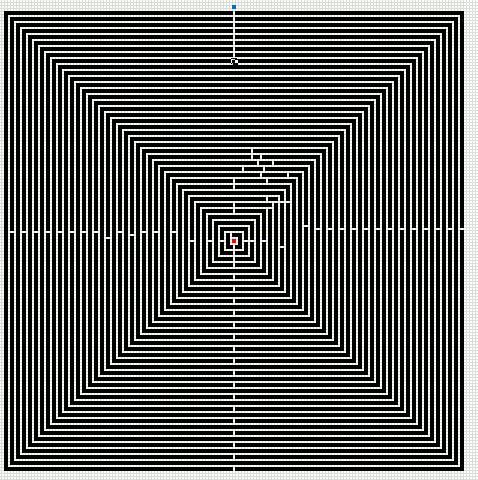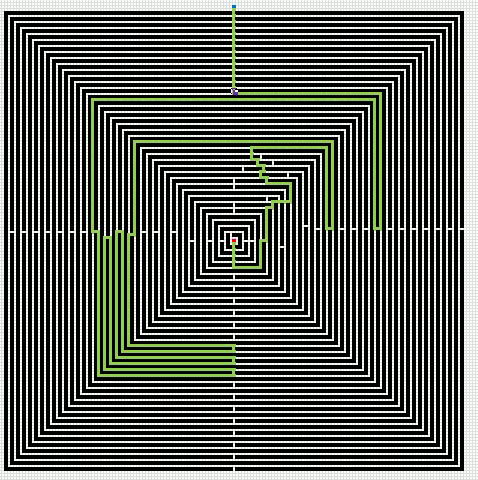
Here is an animated gif showing you a grid 255 * 255 cells. The blue cell is the start cell and it is located almost at the top center. The red cell is the end cell and it is in the middle of the maze. I have walls in this grid, if a cell contains value 1 it is colored black with conditional formatting.
The animation shows me deleting walls and the subroutine finds a new shorter path, highlighted green.
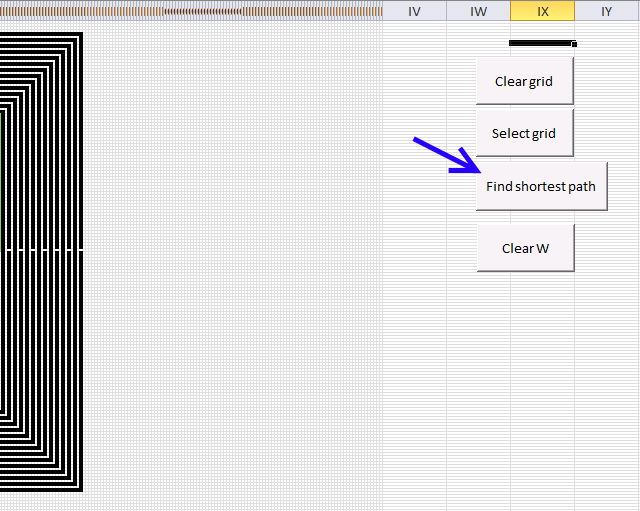
An Event procedure removes the old path and calculates the new path if a cell is changed on this sheet. If you want to remove the even procedure, press with right mouse button on on sheet1. Press with left mouse button on "View Code..". Comment line 3:
Private Sub Worksheet_Change(ByVal Target As Range) Application.EnableEvents = False 'Call FindShortestPath1 Application.EnableEvents = True End Sub
You can start the path optimization manually by press with left mouse button oning the button "Find shortest path".
Button "ClearW" clears the path.
Button "Clear grid" clears everything, start and end point, walls and path.
VBA code
Sub FindShortestPath1()
'This macro shows only the final path
'The defined named range "Area" tells this mcro which cell range to use
Application.ScreenUpdating = False
Dim G() As Variant
Dim H() As Variant
Dim N() As Variant
Dim O() As Variant
Dim C() As Variant
Dim OL() As Variant
Dim CL() As Variant
Dim S() As Variant
Dim E() As Variant
Dim W() As Variant
Dim Gv() As Variant
Dim i As Single
ReDim S(0 To 1)
ReDim E(0 To 1)
ReDim W(0 To 3, 0 To 1)
ReDim OL(0 To 1, 0)
ReDim CL(0 To 1, 0)
ReDim Gv(0 To 3)
Call ClearW
Rng = Range("Area").Value
a = UBound(Rng, 1) - 1
b = UBound(Rng, 2) - 1
ReDim G(0 To a, 0 To b)
ReDim H(0 To a, 0 To b)
ReDim N(0 To a, 0 To b)
ReDim O(0 To a, 0 To b)
ReDim C(0 To a, 0 To b)
'Find start and end coordinates in cell range
For Ri = 1 To UBound(Rng, 1)
For Ci = 1 To UBound(Rng, 2)
If Rng(Ri, Ci) = "S" Then
S(0) = Ri - 1
S(1) = Ci - 1
End If
If Rng(Ri, Ci) = "E" Then
E(0) = Ri - 1
E(1) = Ci - 1
End If
If S(0) <> "" And E(0) <> "" Then Exit For
Next Ci
Next Ri
'Add S to closed list
CL(0, 0) = S(0) 'row
CL(1, 0) = S(1) 'column
'Add values to closed list
W(0, 0) = -1
W(1, 0) = 1
W(2, 0) = 0
W(3, 0) = 0
W(0, 1) = 0
W(1, 1) = 0
W(2, 1) = -1
W(3, 1) = 1
Echk = False
Do Until Echk = True
For i = 0 To UBound(CL, 2)
For j = 0 To 3
chk = False
tr = CL(0, i) + W(j, 0)
tc = CL(1, i) + W(j, 1)
'Check if coordinates are less than 1 or larger than 255
If tr < 0 Or tc < 0 Or tr > UBound(Rng, 1) - 1 Or tc > UBound(Rng, 2) - 1 Then
chk = True
Else
'Check if new coordinates already exist on the closed list
On Error Resume Next
If C(tr, tc) = "C" Then chk = True
If Err <> 0 Then
MsgBox tr & " " & tc
Exit Sub
End If
'Check if coordinate is a wall
If Rng(tr + 1, tc + 1) = 1 Then chk = True
If O(tr, tc) = "O" Then
chk = True
'Calculate G, H and N
If G(CL(0, i), CL(1, i)) + 1 < G(tr, tc) Then
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
N(tr, tc) = G(tr, tc) + H(tr, tc)
End If
End If
'Check if coordinate is NOT on the Open list or Closed list or is a wall
If chk = False Then
'Add coordinates to open list
O(tr, tc) = "O"
OL(0, UBound(OL, 2)) = tr
OL(1, UBound(OL, 2)) = tc
ReDim Preserve OL(UBound(OL, 1), UBound(OL, 2) + 1)
'Calculate G, H and N
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
N(tr, tc) = G(tr, tc) + H(tr, tc)
'Check if cell is End
If Rng(tr + 1, tc + 1) = "E" Then Echk = True
End If
End If
Next j
Next i
'Remove all values in closed list
ReDim CL(0 To 1, 0)
'Find cell(s) in the open list that has the smallest N and add those to the closed list
'Find a value for Nchk
If Echk <> True Then
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(0, i) <> "" Then
Nchk = N(OL(0, i), OL(1, i))
Exit For
End If
Next i
'Find smallest N
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(1, i) <> "" Then
If N(OL(0, i), OL(1, i)) < Nchk And N(OL(0, i), OL(1, i)) <> "" Then
Nchk = N(OL(0, i), OL(1, i))
End If
End If
Next i
'Add cell(s) from open list that has the lowest N, to closed list
Eend = False
For i = LBound(OL, 2) To UBound(OL, 2)
If i <= UBound(OL, 2) Then
On Error GoTo 0
If OL(0, i) <> "" Then
If N(OL(0, i), OL(1, i)) = Nchk Then
Eend = True
If CL(0, 0) <> "" Then ReDim Preserve CL(UBound(CL, 1), UBound(CL, 2) + 1)
C(OL(0, i), OL(1, i)) = "C"
CL(0, UBound(CL, 2)) = OL(0, i)
OL(0, i) = ""
CL(1, UBound(CL, 2)) = OL(1, i)
OL(1, i) = ""
'Remove blank values in open list
For j = i To UBound(OL, 2) - 1
OL(0, j) = OL(0, j + 1)
OL(1, j) = OL(1, j + 1)
Next j
ReDim Preserve OL(UBound(OL, 1), UBound(OL, 2) - 1)
End If
End If
End If
Next i
If Eend = False Then
MsgBox "There is no free path"
Exit Sub
End If
End If
Loop
'Build final path
tr = E(0)
tc = E(1)
Schk = False
Do Until Schk = True
If C(tr + 1, tc) = "C" _
And (Rng(tr + 2, tc + 1) <> "W" _
And Rng(tr + 2, tc + 1) <> "1") _
Then Gv(0) = G(tr + 1, tc)
If C(tr, tc + 1) = "C" _
And (Rng(tr + 1, tc + 2) <> "W" _
And Rng(tr + 1, tc + 2) <> "1") _
Then Gv(1) = G(tr, tc + 1)
If C(tr - 1, tc) = "C" _
And (Rng(tr, tc + 1) <> "W" _
And Rng(tr, tc + 1) <> "1") _
Then Gv(2) = G(tr - 1, tc)
If C(tr, tc - 1) = "C" _
And (Rng(tr + 1, tc) <> "W" _
And Rng(tr + 1, tc) <> "1") _
Then Gv(3) = G(tr, tc - 1)
'Find smallest G
For j = 0 To 3
If Gv(j) <> "" Then Nf = Gv(j)
Next j
For j = 0 To 3
If Gv(j) < Nf And Gv(j) <> "" Then Nf = Gv(j)
Next j
Select Case Nf
Case Gv(0)
tr = tr + 1
Rng(tr + 1, tc + 1) = "W"
Case Gv(1)
tc = tc + 1
Rng(tr + 1, tc + 1) = "W"
Case Gv(2)
tr = tr - 1
Rng(tr + 1, tc + 1) = "W"
Case Gv(3)
tc = tc - 1
Rng(tr + 1, tc + 1) = "W"
End Select
If Rng(tr + 2, tc + 1) = "S" _
Or Rng(tr + 1, tc + 2) = "S" _
Or Rng(tr, tc + 1) = "S" _
Or Rng(tr + 1, tc) = "S" Then Schk = True
Loop
Range("Area") = Rng
Application.ScreenUpdating = True
End Sub
You may find these posts interesting
- Finding the shortest path – A * pathfinding
- Customize excel maze
- Solve a maze
- Build a maze
- Shortest path
Get excel *.xlsm file
Pathfinding category
What's on this page Finding the shortest path - A * pathfinding Optimize pick path in a warehouse 1. […]
Excel categories
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.