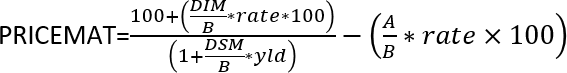Financial functions – PMT to RATE
Table of Contents
1. How to use the PMT function
What is the PMT function?
The PMT function returns the payment amount needed for borrowing a fixed sum of money based on constant payments (annuity) and interest rate.
You can also use the PMT function to calculate the amount to save each period to reach a given sum, based on an interest rate and the number of periods.
What is the principal?
The principal is the amount you have to pay back and interest is the charges you pay for borrowing the money.
What is an investment?
An investment is an asset or business acquired with the goal of generating income or appreciation, the purpose is to grow the money over time.
What are periods?
A payment period is the length of time between payments made on a loan or investment. For example, a loan with monthly payments the payment period would be one month. A loan with quarterly payments the payment period would be three months.
What is present value?
The present value is the initial amount that will earn interest/dividend.
What is future value?
The compounded amount after the calculated periods based on the given rate. It measures what a current capital (present value) amount will be worth at a designated future date.
What are periodic constant payments?
Periodic constant payments are payments that are made at regular intervals such as monthly, quarterly, or yearly and have the same amount each time.
What is a constant interest rate?
A fixed interest rate is an interest rate that remains the same throughout the term of a loan or an investment.
What is the number of compounding periods per year?
The number of compounding periods per year refers to how often interest is compounded annually on an investment or loan.
Some common compounding periods:
- Annually - 1 compounding period per year
- Semiannually - 2 compounding periods per year
- Quarterly - 4 compounding periods per year
- Monthly - 12 compounding periods per year
- Weekly - 52 compounding periods per year
- Daily - 365 compounding periods per year
What is compounding?
Compounding refers to the process of generating more interest from interest that was previously earned. It causes interest to grow exponentially over time.
Related functions
| Function | Description |
|---|---|
| PMT(rate, nper, pv, [fv], [type]) | Returns the payment amount needed for borrowing a fixed sum of money based on constant payments (annuity) and interest rate. |
| PPMT(rate, per, nper, pv, [fv], [type]) | Calculates the principal payment for a specific period for an investment based on repeated constant payments and a constant interest rate. |
| IPMT(rate, per, nper, pv, [fv], [type]) | Calculates the interest payment for a specific period for an investment based on repeated constant payments and a constant interest rate. |
| ISPMT(rate, per, nper, pv) | Calculates the interest paid during a specific period of an investment. |
Table of Contents
- PMT Function Syntax
- PMT Function Arguments
- PMT Function example
- Excel loan calculator
- Loan calculator - extra payment
- Calculate running total interest paid
- Calculate running total principal paid
- Calculate the interest saved saved by making extra payments?
- Calculate the months saved by making extra payments?
- I know the loan payment, interest rate, and term. How do I calculate the loan amount?
- Get Excel file
1. PMT Function Syntax
PMT(rate, nper, pv, [fv], [type])
2. PMT function Arguments
| Rate | Required. The interest rate. |
| nper | Required. The number of payments. |
| pv | Required. The present value. |
| [fv] | Optional. The future value. Default value is 0 (zero). |
| [type] | Optional. When payments are due, default value is 0 (zero).
0 (zero) : at the end of the period. 1 : at the beginning of the period. |
Think carefully about what period you use (years, quarterly, months, weekly, days or whatever unit) before you specify the number of payments (nper) and the interest rate.
Monthly payments: For a ten-year loan at an annual interest rate of 5 percent use 5%/12 (rate) and 10*12 (nper).
Annual payments: For a ten-year loan at an annual interest rate of 5 percent use 5% (rate) and 10 (nper).
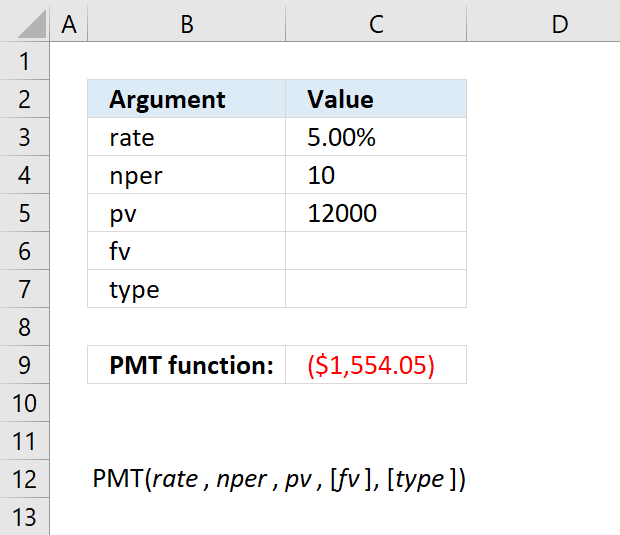
3. PMT Function example
The above image shows the annual payment needed for a 10-year $12,000 loan based on a 5 percent interest rate.
Formula in cell C7:
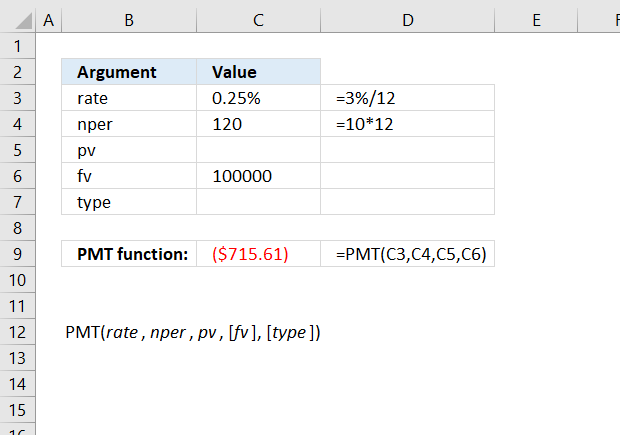
The image above demonstrates how to calculate the monthly savings amount needed to reach 100,000 with a 3% interest rate and 10 years of savings.
Formula in cell C9:
4. Excel Loan Calculator
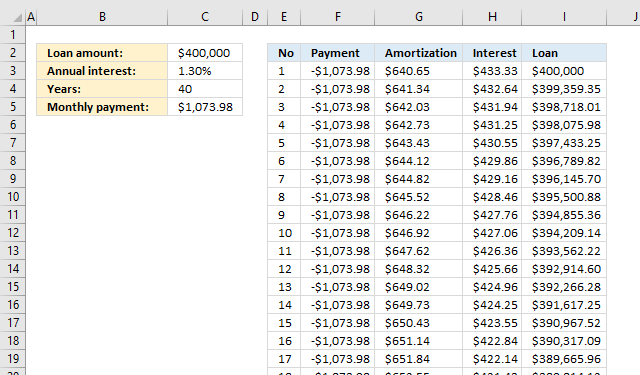
The image above describes a loan calculator that displays payment, amortization or principal, interest, and remaining loan per month. The formulas in column E to I resize appropriately based on the values you enter in C2:C4.
| Loan amount | This is the total amount you borrow, this can be, for example, a mortgage. |
| Annual interest | A percentage that you will pay for the loan annually. |
| Years | For how long the loan will be paid. |
| Monthly payment | This cell is calculated by Excel using the PMT function, don't enter a value here. |
4.1 Calculate the monthly payment
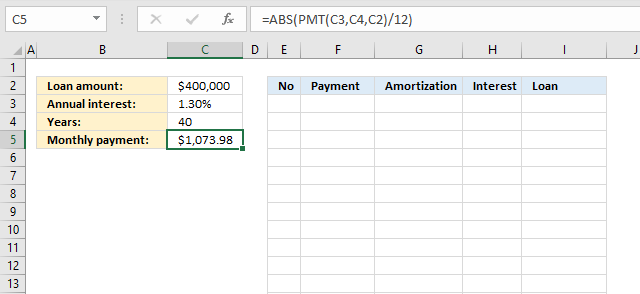
Formula in cell C5:
Explaining formula in cell E4
Step 1 - Calculate yearly payment
The PMT function has the following arguments: PMT(rate, nper, pv, [fv], [type])
rate - interest rate
nper - number of payments
pv - present value
The interest rate is annual. The number of payments is once per year for 40 years. The present value is 400000.
PMT(C3,C4,C2)
becomes
PMT(0.013, 40, 400000)
and returns -12887.7516044148.
Step 2 - Calculate monthly payment
Divide yearly payment with 12 to calculate the monthly payment.
PMT(C3,C4,C2)/12
becomes
-12887.7516044148/12
and returns -1073.9793003679.
Step 3 - Remove sign
The PMT function returns a negative value meaning the amount will be subtracted from your account. The ABS function removes the sign, we don't need the negative sign in our calculations.
ABS(PMT(C3,C4,C2)/12)
becomes
ABS(-1073.9793003679)
and returns 1073.9793003679.
4.2 Create a series of numbers representing months
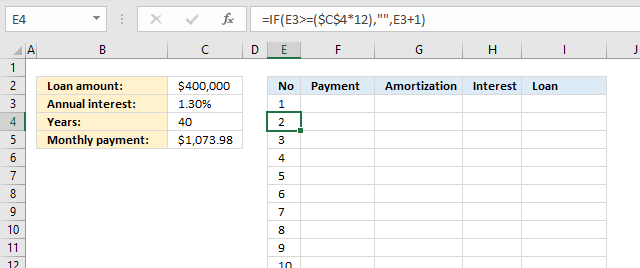
Value in cell E3:
Formula in cell E4:
Copy cell E4 and paste to cells below as far as needed.
Explaining formula in cell E4
Step 1 - Calculate months needed to pay back loan
$C$4*12
becomes
40*12 equals 480.
Step 2 - Check if the cell above is equal or larger than the number of months
The parentheses allow us to control the order of operation. We want to calculate $C$4*12 before we evaluate if the value in cell E3 is larger than or equal to.
E3>=($C$4*12)
becomes
E3>=480
becomes
1>=480
and returns FALSE.
Step 3 - Evaluate IF function
The IF function returns one value if the logical test is TRUE and another value if the logical test is FALSE.
IF(logical_test, [value_if_true], [value_if_false])
The IF function allows us to add 1 to cell E3 if E3 is smaller than or equal to the number of payments needed.
IF(E3>=($C$4*12),"",E3+1)
becomes
IF(FALSE,"",E3+1)
becomes
IF(FALSE,"",1+1)
and returns 2 in cell E4.
4.3 Populate column F with payments
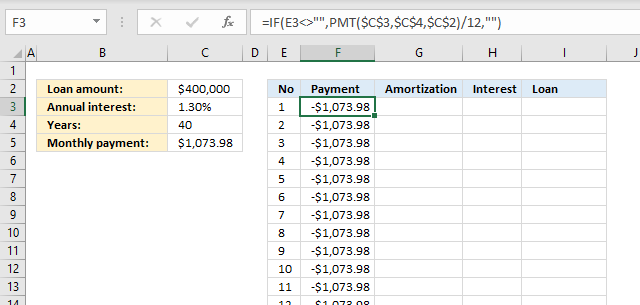
Formula in cell F3:
Explaining formula in cell F3
Step 1 - Calculate monthly payment
The cell references below are absolute cell references, they don't change when we copy the cell and paste to cells below.
PMT($C$3,$C$4,$C$2)
becomes
PMT(0.013, 40, 400000)
and returns -12887.7516044148.
Step 2 - Divide with 12
PMT($C$3,$C$4,$C$2)/12
becomes
-12887.7516044148/12
and returns -1073.9793003679
Step 3 - Check if adjacent cell is not empty
The IF function makes sure that the adjacent cell in column E is not empty, we don't want to continue calculating when there are no more months.
IF(E3<>"",PMT($C$3,$C$4,$C$2)/12,"")
becomes
IF(1<>"",PMT($C$3,$C$4,$C$2)/12,"")
becomes
IF(TRUE,PMT($C$3,$C$4,$C$2)/12,"")
becomes
IF(TRUE,-1073.9793003679,"")
and returns -1073.9793003679.
4.4 Calculate amortization
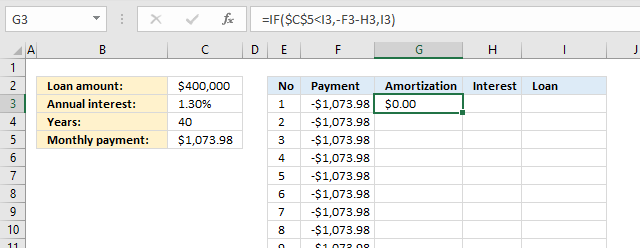
The formula in cell G3 returns 0 (zero) now but will return a number when the formulas in cell H3 and I 3 are populated.
Formula in cell G3:
Explaining formula in cell G3
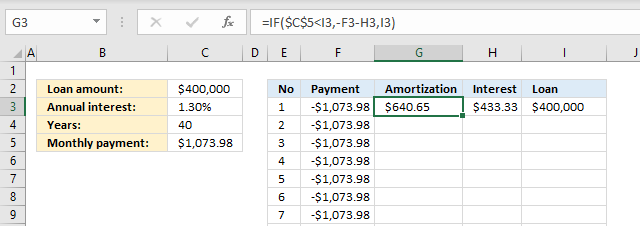
Formulas in cell H3 and I3 are explained in the next section. They are populated now in order to explain the calculation in cell G3.
Step 1 - Check if remaining loan is larger than monthly payment
The larger than character checks if cell I3 is larger than cell C5. Note that the dollar signs are important here. They make the cell reference to cell C5 absolute meaning it does not change when we copy the cell and paste to cells below.
$C$5<I3
becomes
1073.9793003679<400000
and returns TRUE.
Step 2 - Calculate amortization
The IF function returns one value if the logical test is TRUE and another value if the logical test is FALSE.
IF(logical_test, [value_if_true], [value_if_false])
IF($C$5<I3,-F3-H3,I3)
becomes
IF(TRUE,-F3-H3,I3)
becomes
IF(TRUE,-1073.9793003679-433.333333333333,I3)
and returns 640.645967034566
4.5 Calculate interest per month
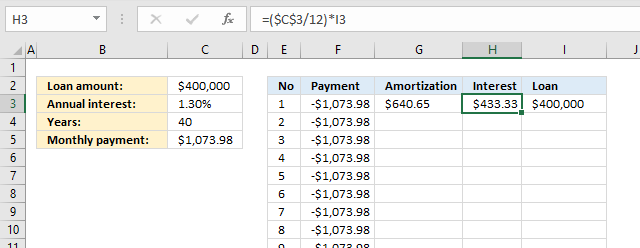
Formula in cell H3:
Explaining formula in cell H3
Step 1 - Divide annual interest with 12
There a re 12 months in a year, to get the monthly interest we divide the annual interest with 12.
$C$3/12
becomes
0.013/12
and returns 0.00108333333333333.
Step 2 - Multiply with loan
$C$3/12*I3
becomes
0.00108333333333333*I3
becomes
0.00108333333333333*400000
and returns 433.333333333333.
4.6 Calculate remaining loan per month
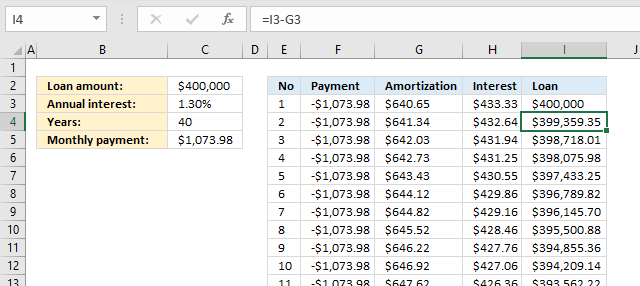
Formula in cell I3:
Formula in cell I4:
The formula in cell I4 takes the loan in cell I3 and subtracts with the amortization in cell G3.
5. Loan calculator - extra payment
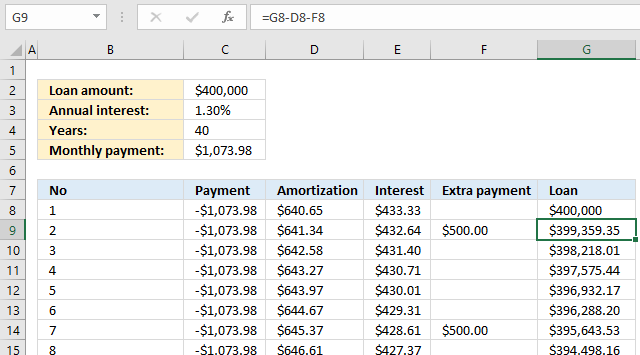
The loan schedule shown in the image above allows you to do extra payments, type them in column F and the formula in column G takes care of the calculations.
The only formula that changes compared to the loan calculator above is the formula in column G.
Formula in cell G9:
The formula in cell G9 takes the loan amount in cell G8 and subtracts with the amortization in cell D8 and the extra payment in cell F8.
Copy cell G9 and paste to cells below as far as needed. The other formulas are explained here: Loan schedule calculator
6. Calculate running total interest paid
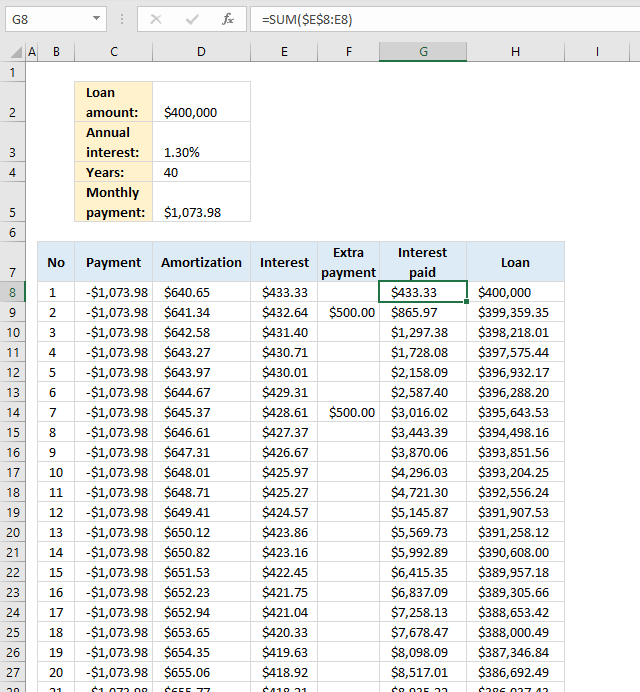
The image above demonstrates a formula in column G that displays the sum of interest paid, in other words, a running total of interest paid.
Formula in cell G8:
Explaining formula in cell G8
Step 1 - Cell reference
Combine an absolute and relative cell reference and you get an expanding cell reference. It grows when you copy the cell and paste to cells below as far as needed.
$E$8:E8 returns 433.33.
Step 2 - Sum values
The SUM function adds numbers from a cell range and returns a total.
SUM($E$8:E8)
becomes
SUM(433.33)
and returns 433.33 in cell G8.
7. Calculate running total principal paid
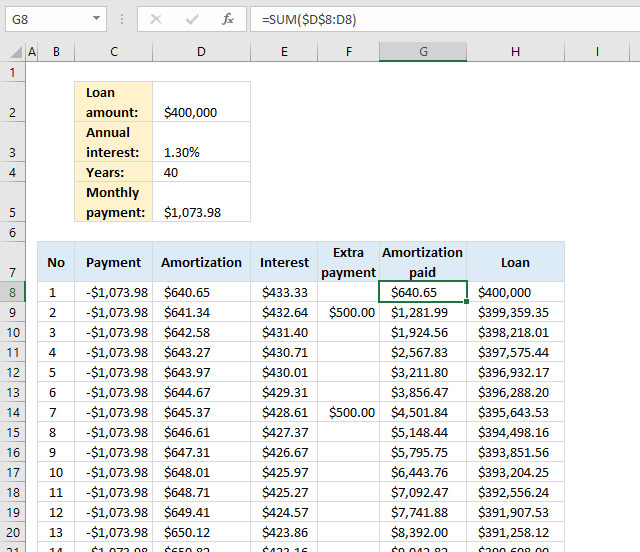
The image above demonstrates a formula in column G that displays the sum of principal paid, in other words, a running total of principal paid.
Formula in cell G8:
Use the following formula in cell G8 if you want to include extra payments to amortization total:
Check formula explanation here: Calculate running total interest paid
8. Calculate the interest saved by making extra payments?
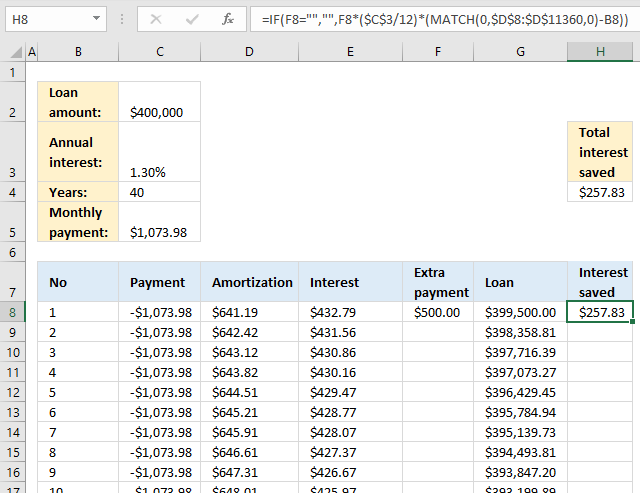
The formula in cell H8 calculates the saved interest based on the amount of the extra payment specified in cell F8.
Formula in cell H8:
Explaining formula in cell H8
Step 1 - Calculate interest per month
The value in cell C3 is the annual interest. Divide with 12 to get the monthly interest. $C$3 is an absolute cell reference, it stays the same when we copy the cell and paste it to cells below.
$C$3/12
becomes
0.013/12 equals 0.00108333333333333.
Step 2 - Multiply with amount
F8*($C$3/12)
becomes
F8*0.00108333333333333
becomes
500*0.00108333333333333
and returns 0.541666666666667.
Step 3 - Find first amortization that is zero
The MATCH function returns the relative position of a given value in an array or cell range.
MATCH(0,$D$8:$D$11360,0)
returns 477.
Step 4 - Subtract current month with last month
(MATCH(0,$D$8:$D$11360,0)-B8)
becomes
477 - 1 equals 476.
Step 5 - Multiply values
F8*($C$3/12)*(MATCH(0,$D$8:$D$11360,0)-B8)
becomes
0.541666666666667*476
and returns 257.833333333333.
Step 6 - Check if cell F8 is empty
IF(F8="","",F8*($C$3/12)*(MATCH(0,$D$8:$D$11360,0)-B8))
becomes
IF(FALSE,"",F8*($C$3/12)*(MATCH(0,$D$8:$D$11360,0)-B8))
becomes
IF(FALSE,"",257.833333333333)
and returns 257.833333333333.
9. Calculate the months saved by making extra payments?
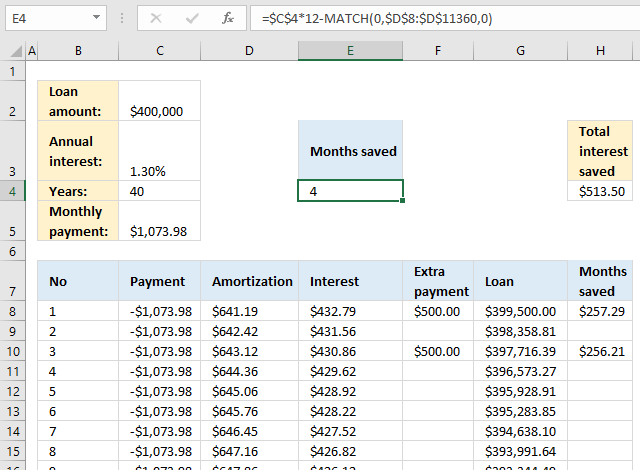
The formula in cell E4 calculates the saved months based on the amounts of the extra payments specified in column F.
Formula in cell H8:
Explaining formula in cell H8
Step 1 - Calculate total months
$C$4*12
becomes
40*12 equals 480.
Step 2 - Calculate months needed to repay the loan
The MATCH function returns the relative position of a given value in an array or cell range.
The MATCH function finds the first cell that equals to 0 (zero) in cell range $D$8:$D$11360.
MATCH(0,$D$8:$D$11360,0)
and returns 476.
Step 3 - Subtract total with months needed
$C$4*12-MATCH(0,$D$8:$D$11360,0)
becomes
480 - 476 equals 4.
10. I know the loan payment, interest rate, and term. How do I calculate the loan amount?
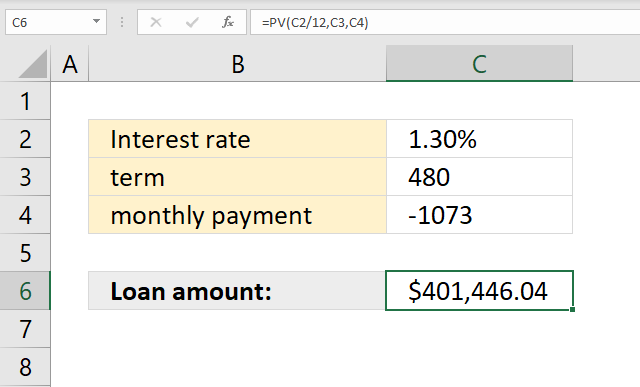
The image above demonstrates a formula in cell C6 that calculates the loan amount based on an interest rate, the number of months needed to repay the loan and the monthly payment.
Formula in cell C6:
The PV function calculates the present value of a loan.
PV(rate, nper, pmt, [fv], [type])
Useful links
PMT function - Microsoft support
Excel Formula Coach
Payment Calculator
2. How to use the PPMT function
What is the PPMT function?
The PPMT function calculates the principal payment for a specific period for an investment based on repeated constant payments and a constant interest rate.
What is the principal?
The principal is the amount you have to pay back and interest is the charges you pay for borrowing the money.
What is an investment?
An investment is an asset or business acquired with the goal of generating income or appreciation, the purpose is to grow the money over time.
What are periods?
A payment period is the length of time between payments made on a loan or investment. For example, a loan with monthly payments the payment period would be one month. A loan with quarterly payments the payment period would be three months.
What is present value?
The present value is the initial amount that will earn interest/dividend.
What is future value?
The compounded amount after the calculated periods based on the given rate. It measures what a current capital (present value) amount will be worth at a designated future date.
What are periodic constant payments?
Periodic constant payments are payments that are made at regular intervals such as monthly, quarterly, or yearly and have the same amount each time.
What is a constant interest rate?
A fixed interest rate is an interest rate that remains the same throughout the term of a loan or an investment.
What is the number of compounding periods per year?
The number of compounding periods per year refers to how often interest is compounded annually on an investment or loan.
Some common compounding periods:
- Annually - 1 compounding period per year
- Semiannually - 2 compounding periods per year
- Quarterly - 4 compounding periods per year
- Monthly - 12 compounding periods per year
- Weekly - 52 compounding periods per year
- Daily - 365 compounding periods per year
What is compounding?
Compounding refers to the process of generating more interest from interest that was previously earned. It causes interest to grow exponentially over time.
Related functions
| Function | Description |
|---|---|
| PMT(rate, nper, pv, [fv], [type]) | Returns the payment amount needed for borrowing a fixed sum of money based on constant payments (annuity) and interest rate. |
| PPMT(rate, per, nper, pv, [fv], [type]) | Calculates the principal payment for a specific period for an investment based on repeated constant payments and a constant interest rate. |
| IPMT(rate, per, nper, pv, [fv], [type]) | Calculates the interest payment for a specific period for an investment based on repeated constant payments and a constant interest rate. |
| ISPMT(rate, per, nper, pv) | Calculates the interest paid during a specific period of an investment. |
PPMT function Syntax
PPMT(rate, per, nper, pv, [fv], [type])
PPMT function Arguments
| rate | Required. The interest rate. |
| per | Required. The period. |
| nper | Required. The total number of periods in an annuity.
Examples: |
| pv | Required. Present value. |
| [fv] | Optional. Future value, default value is 0 (zero). |
| [type] | Optional. When payments are due.
0 - End of period, default value. |
Use the same unit for rate and nper, the above example uses monthly payments. That is why the interest rate is divided by 12 and nper is multiplied by 12. There are 120 monthly payments in a 10 year period.
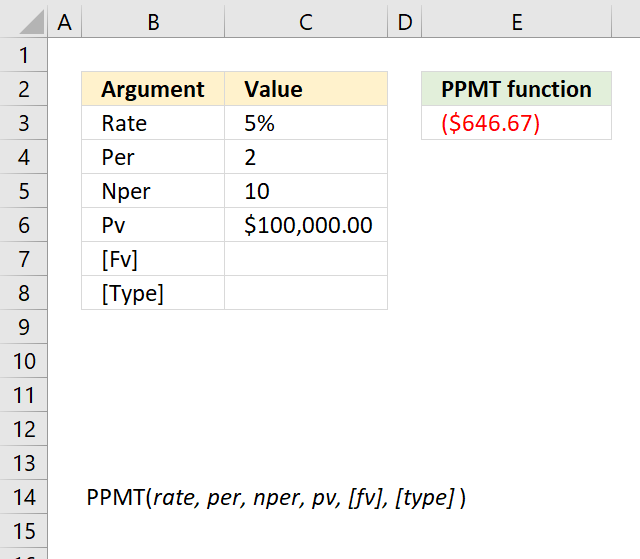
PPMT function example
The image above shows the PPMT function in cell E3 calculating the principal for the second month for a 10 year loan of 100 000.
Formula in cell E3:
PPMT function not working
How is the PPMT function calculated?
3. How to use the PRICEMAT function
What is the PRICEMAT function?
The PRICEMAT function calculates the price per $100 nominal value of a bond that pays interest at maturity.
What is the nominal value for a bond?
The nominal value, also called the par value or face value, is the amount a bond is issued and redeemed for by the bond issuer. It's the stated value of the bond.
What is interest?
Interest refers to the periodic coupon payments made by a bond issuer to bondholders over the bond's lifetime. However, the PRICEMAT function works for bonds that pay interest at maturity.
What is bond maturity?
Bond maturity is the date when a bond's term ends, at which point the issuer must repay the bond's par value and any final interest due to bondholders. A 30-year bond issued today will have a maturity date 30 years from now.
PRICEMAT function Syntax
PRICEMAT(settlement, maturity, issue, rate, yld, [basis])
PRICEMAT function Arguments
| settlement | Required. The bond's settlement date. |
| maturity | Required. The bond's maturity date, in other words, when it expires. |
| issue | Required. The bond's issue date. |
| rate | Required. The bond's interest rate at date of issue. |
| yld | Required. The bond's annual return. |
| [basis] | Optional. Day count basis.
0 (zero) - US (NASD) 30/360 (default value) 1 - Actual/actual 2 - Actual/360 3 - Actual/365 4 - European 30/360 |
What is the bond's settlement date?
A bond's settlement date is the date when the trade is finalized and the bond is delivered to the buyer in exchange for payment to the seller. Settlement for US treasury bonds is usually T+1 day.
What is the bonds issue date?
A bond's issue date is the original date when the bond was first offered and sold to investors on the primary market by the issuing entity. The bond's coupon payment schedules are aligned with the issue date.
What is the bond's interest rate at date of issue?
The interest rate at a bond's issue date, also called the coupon rate, is the annual interest rate the bond will pay throughout its lifetime based on the bond's par value. A 5% coupon rate means the bond will pay 5% of par annually.
What is the bond's annual return?
A bond's annual return is the gain or loss in value over a one year holding period plus any interest income. It factors in both bond price appreciation/depreciation and the interest coupons received.
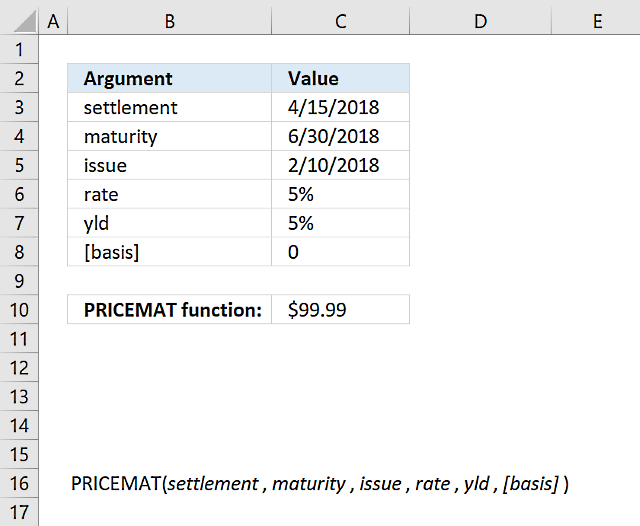
PRICEMAT function example
Formula in cell C10:
PRICEMAT function not working
Settlement, maturity, issue, and basis are shortened to integers.
The PRICEMAT function returns:
#NUM! error value if
rate < 0
yld < 0
basis < 0
basis > 4
settlement >= maturity
#VALUE! error value if
settlement, issue or maturity is not a valid date. Use the DATE function in the PRICEMAT function to avoid errors. Example DATE(2010, 11, 5) is 5th November, 2010.
How is the PRICEMAT function calculated?
The following formula demonstrates how the PRICEMAT function calculates.
| B | Days in year. |
| DSM | Days from settlement to maturity. |
| DIM | Number of days from issue to maturity. |
| A | Number of days from issue to settlement. |
4. How to use the PV function
The PV function calculates the net present value for an investment or loan. PV stands for present value.
What is an investment?
An investment is an asset or business acquired with the goal of generating income or appreciation, the purpose is to grow the money over time.
What are periods?
A payment period is the length of time between payments made on a loan or investment. For example, a loan with monthly payments the payment period would be one month. A loan with quarterly payments the payment period would be three months.
What is present value?
The present value is the initial amount that will earn interest/dividend.
What is future value?
The compounded amount after the calculated periods based on the given rate. It measures what a current capital (present value) amount will be worth at a designated future date.
What are periodic constant payments?
Periodic constant payments are payments that are made at regular intervals such as monthly, quarterly, or yearly and have the same amount each time.
What is a constant interest rate?
A fixed interest rate is an interest rate that remains the same throughout the term of a loan or an investment.
What is the number of compounding periods per year?
The number of compounding periods per year refers to how often interest is compounded annually on an investment or loan.
Some common compounding periods:
- Annually - 1 compounding period per year
- Semiannually - 2 compounding periods per year
- Quarterly - 4 compounding periods per year
- Monthly - 12 compounding periods per year
- Weekly - 52 compounding periods per year
- Daily - 365 compounding periods per year
Related functions
| Function | Description |
|---|---|
| RATE(nper, pmt, pv, [fv], [type]) | Returns the interest rate per period of an annuity |
| PV(rate, nper, pmt, [fv], [type]) | Returns the present value of an investment. |
| FV(rate, nper, pmt, [pv], [type]) | Returns the future value of an investment. |
| PDURATION(rate, pv, fv) | Returns the periods needed for an investment to reach a future value. |
What's on this webpage
- PV Function Syntax
- PV Function Arguments
- PV Function example
- What is the formula behind the PV function?
- How is the result of the PV function calculated in detail?
- What amount is needed if I want x in future value, the interest rate is constant, and the number of periods is given?
- What amount is needed if I want x in future value, the interest rate is constant, the payment amount, and the number of periods are given?
- How much can I borrow if I can pay x per month and the interest is y? (Link)
- Get Excel file
1. PV Function Syntax
PV(rate, nper, pmt, [fv], [type])
2. PV Function Arguments
| rate | Required. The interest rate per period. If nper is years then the interest rate is per year. Divide the interest rate with 12 if you use months in the nper argument. |
| nper | Required. The total number of payment periods in an annuity. |
| pmt | Required. The payment amount per period. Interest and principal is often included in this amount but not other fees or taxes. The pmt argument is not used if you use the [fv] argument. |
| [fv] | Optional. The future value. |
| [type] | Optional. The number 0 or 1 and indicates when payments are due. |
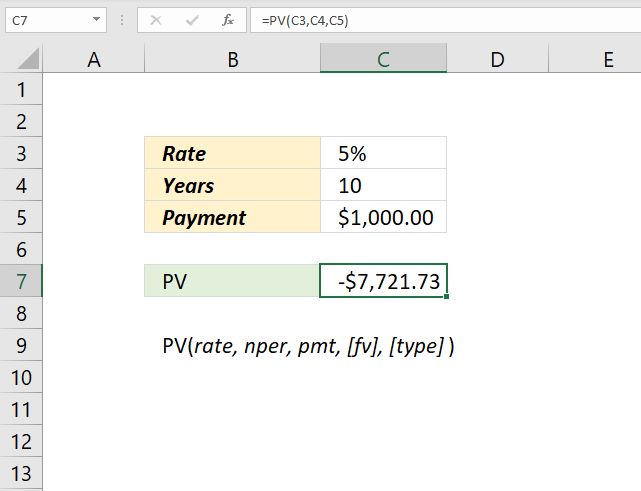
3. PV Function example

Formula in cell C7:
4. What is the formula behind the PV function?
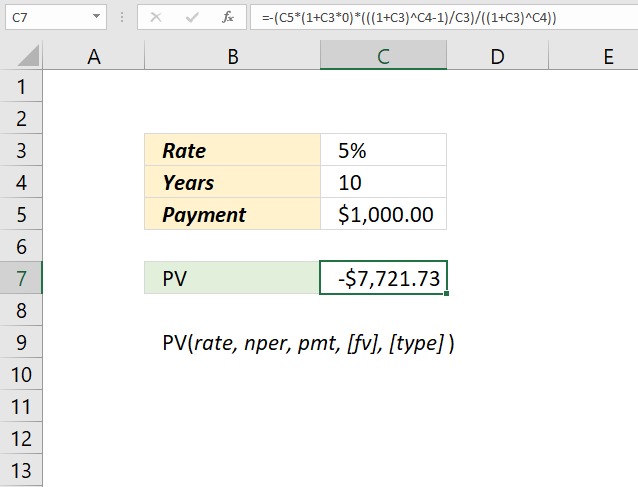
Formula:
Formula in cell C7:
5. How is the result of the PV function calculated in detail?
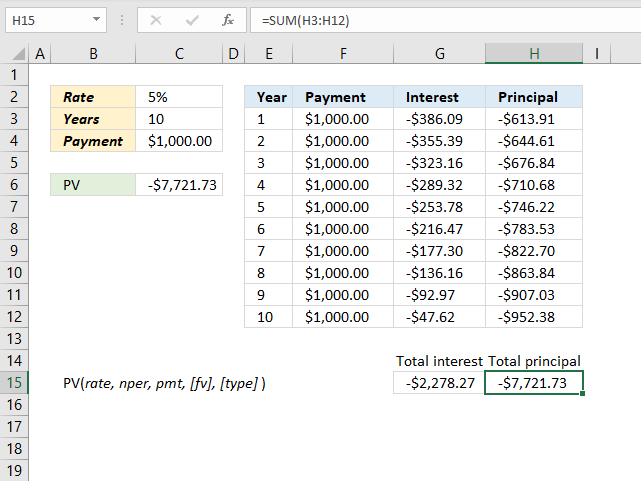
The PV function in cell C6 calculates the present value of an annuity loan or the amount you can borrow when the interest rate is 5% per year and the loan is paid back in ten years. In other words, it calculates how much the loan is based on a given interest rate, how much you pay per period, and the amount you pay per period.
An annuity loan is paid back for a specific time range at a given interest rate with the same amount for all payments.
The table in cell range E2:H12 shows interest and principal for each period based on values in cell range C2:C4. The total principal (or amortization) paid is the same as the present value in cell C6, which is needed to pay back the entire loan.
Formula in cell C6:
The result in cell C6 is the present value of the loan based on the interest rate, periods, and payment amount.
The formula in cell G3 calculates the interest included in each payment.
Formula in cell G3:
The principal is what's left after the interest is paid, it is calculated in cell h3.
Formula in cell H3:
The formulas in cell G15 and H15 adds the amounts and return the total of interest and principal respectively.
Formula in cell G15:
Formula in cell H15:
6. What anount is needed if I want x in future value, the interest rate is constant, and the number of periods is given?
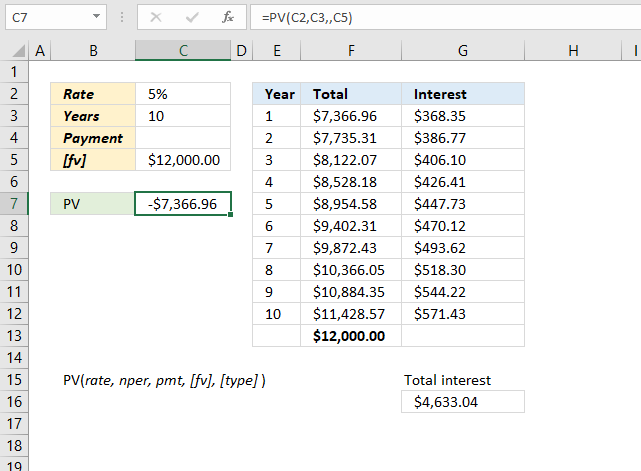
The image above demonstrates how to use the PV function when you want to know the amount needed for an investment when the interest rate is specified, and the number of periods are given.
Formula in cell C7:
Note that the pmt argument can be empty when you specify the fv (future value) argument in the PV function.
The table, shown in the image above, displays the start amount and the interest for each period. The total accumulates the interest (column F) and the fv (future value) is reached after the given period. The table is not needed for the calculation, it is only there to show that the numbers add up and are correct.
See cell F13, it is equal to the future value in cell C5.
Formula in cell F3:
Copy cell F3 and paste cells below.
Formula in cell G3:
Copy cell G3 and paste cells below.
7. What amount is needed if I want x in future value, the interest rate is constant, the payment amount, and the number of periods are given?
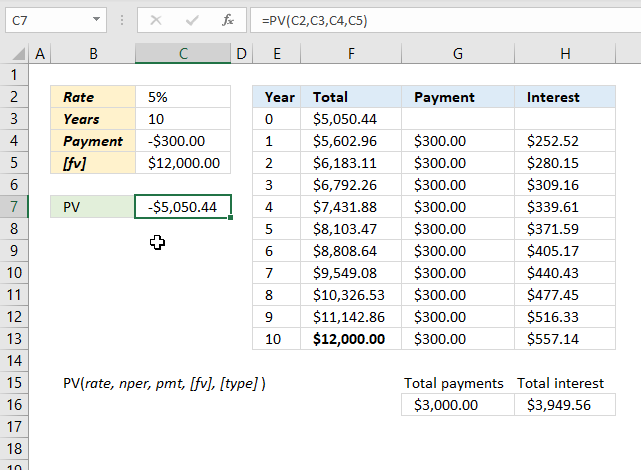
The image above shows what amount is needed if you save x amount for each period to reach a future value [fv) given a constant interest rate.
Formula in cell C7:
The table in cell range E2:H13 shows that the numbers add up to the future value, specified in cell C5, after the given time of periods based on a constant interest rate.
The table is not needed to calculate the present value of the investment, the PV function is all that is needed.
Formula in cell F3:
Copy cell F3 and paste to cells below as far as needed.
Formula in cell G4:G13:
Formula in cell H4:
Copy cell H4 and paste to cells below as far as needed.
Useful links
PV function - Microsoft support
Excel Formula Coach - find the present value of a loan
Present Value Calculator
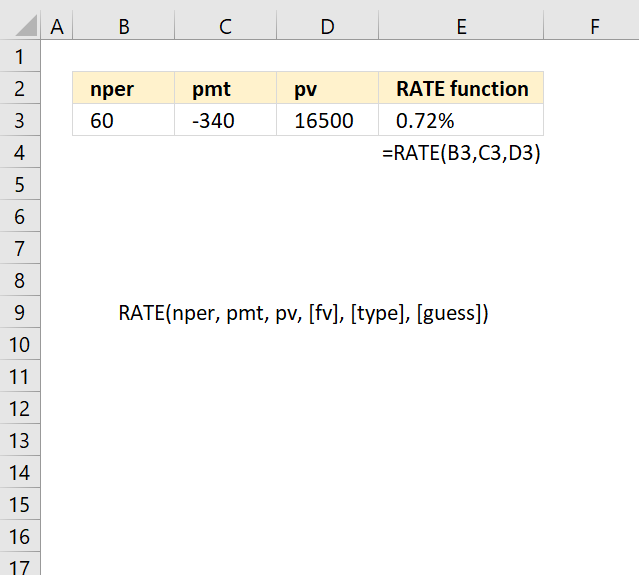
5. How to use the RATE function
What is the RATE function?
The RATE function returns the interest rate per period of an annuity.
What is an investment?
An investment is an asset or business acquired with the goal of generating income or appreciation, the purpose is to grow the money over time.
What are periods?
A payment period is the length of time between payments made on a loan or investment. For example, a loan with monthly payments the payment period would be one month. A loan with quarterly payments the payment period would be three months.
What is present value?
The present value is the initial amount that will earn interest/dividend.
What is future value?
The compounded amount after the calculated periods based on the given rate. It measures what a current capital (present value) amount will be worth at a designated future date.
What are periodic constant payments?
Periodic constant payments are payments that are made at regular intervals such as monthly, quarterly, or yearly and have the same amount each time.
What is a constant interest rate?
A fixed interest rate is an interest rate that remains the same throughout the term of a loan or an investment.
What is the number of compounding periods per year?
The number of compounding periods per year refers to how often interest is compounded annually on an investment or loan.
Some common compounding periods:
- Annually - 1 compounding period per year
- Semiannually - 2 compounding periods per year
- Quarterly - 4 compounding periods per year
- Monthly - 12 compounding periods per year
- Weekly - 52 compounding periods per year
- Daily - 365 compounding periods per year
What is compounding?
Compounding refers to the process of generating more interest from interest that was previously earned. It causes interest to grow exponentially over time.
Related functions
| Function | Description |
|---|---|
| RATE(nper, pmt, pv, [fv], [type]) | Returns the interest rate per period of an annuity |
| PV(rate, nper, pmt, [fv], [type]) | Returns the present value of an investment. |
| FV(rate, nper, pmt, [pv], [type]) | Returns the future value of an investment. |
| PDURATION(rate, pv, fv) | Returns the periods needed for an investment to reach a future value. |
RATE function Syntax
RATE(nper, pmt, pv, [fv], [type], [guess])
RATE function Arguments
| nper | Required. The total number of payment periods in an annuity. |
| pmt | Required. The payment made each period and cannot change over the life of the annuity. Typically, pmt includes principal and interest but no other fees or taxes. If pmt is omitted, you must include the fv argument. |
| pv | Required. The present value — the total amount that a series of future payments is worth now. |
| [fv] | Optional. The future value, or a cash balance you want to attain after the last payment is made. If fv is omitted, it is assumed to be 0 (the future value of a loan, for example, is 0). If fv is omitted, you must include the pmt argument. |
| [type] | Optional. The number 0 or 1 and indicates when payments are due. |
| [guess] | Optional. Your guess for what the rate will be. |
RATE Function example
Formula in cell E3:
RATE Function not working
The RATE function uses an iterative process (repeated calculations) to find the interest rate result, this means it may have more than one possible solution for the rate.
The RATE function will display the #NUM! error value if after trying 20 times at narrowing down the rate via repeated guesses and the results are still not consistent within 0.0000001
How is the RATE Function calculated?
The math formula behind the RATE function is:
Rate = (Fv/Pv)(1/nper)
Fv - future value
Pv - present value
nper - periods
Excel categories
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.