How to use the ACCRINTM function
What is the ACCRINTM function?
The ACCRINTM function calculates the accrued interest for a security that pays interest at maturity. ACCRINTM stands for accrued interest at maturity.
Table of Contents
1. Introduction
What is a security?
A security that pays interest is a bond that investors use to loan money to a company or a government in exchange for interest payments. The interest rate is fixed and does not change over the life of the security.
What is accrued interest?
In finance, accrued interest is the interest on a bond that has accumulated since the last coupon payment.
What is the difference between the ACCRINT function and ACCRINTM function?
ACCRINT function calculates the accrued interest paid by the issuer periodically while the ACCRINTM calculates the interest that is paid at maturity.
For example, the arguments show the differences between these two functions:
ACCRINT(issue_date, first_interest, settlement, rate, par, frequency)
ACCRINTM(issue, settlement, rate, par, [basis])
What is the maturity date of a security?
The maturity date is the future date when the financial instrument expires or terminates. For bonds, it's when the principal investment is repaid to the investor.
For example, a 5-year bond issued today in 2023 will have a maturity date of 2028. That's when the original bond investment will be returned after the 5 years is up.
What is the security's issue date?
The issue date of a security is the date that the security was first issued or sold to investors. For bonds, the issue date is the date the bond was first offered and sold by the issuing entity. It establishes when the security's term or maturity period begins. The issue date starts the clock for calculating payments like interest or dividends.
What is the the security's settlement date?
The settlement date of a security is the date that the trade is finalized and the buyer must make payment to complete the transaction.
What is the security's annual coupon rate?
The annual coupon rate is the interest rate that a bond issuer pays annually to bondholders based on the face value of the bond. It is stated as a percentage of the bond's par value. The coupon rate is set when the bond is first issued and generally doesn't change.
What is the security's par value?
The par value, or face value, of a security is the nominal value or dollar amount assigned to the security by the issuer. Par value is the amount the bondholder receives back at maturity.
What is the math behind the ACCRINTM function?
The ACCRINTM function calculates the accrued interest for a security that pays interest at maturity using the following formula:
ACCRINTM = par × rate × (A / D)
Where:
- par is the par value (face value) of the security.
- rate is the annual coupon rate.
- A is the number of accrued days counted according to a monthly basis. For securities that pay interest at maturity A represents the number of days from the issue date to the maturity date.
- D is the annual year basis which is the number of days in a year used for day-count conventions (e.g., 360 days for a 30/360 basis, 365 days for an actual/365 basis).
2. Syntax
ACCRINTM(issue, settlement, rate, par, [basis])
| issue | Required. The security's issue date. |
| settlement | Required. The security's settlement date. The security settlement date is the date after the issue date when the security is traded to the buyer. |
| rate | Required. The security's annual coupon rate. |
| par | Required. The security's par value. Default value is $1,000. |
| [basis] | Optional. The type of day count basis to use. |
| Basis | Day count basis |
|---|---|
| 0 (default value) | US (NASD) 30/360 |
| 1 | Actual/actual |
| 2 | Actual/360 |
| 3 | Actual/365 |
| 4 | European 30/360 |
3. Example 1

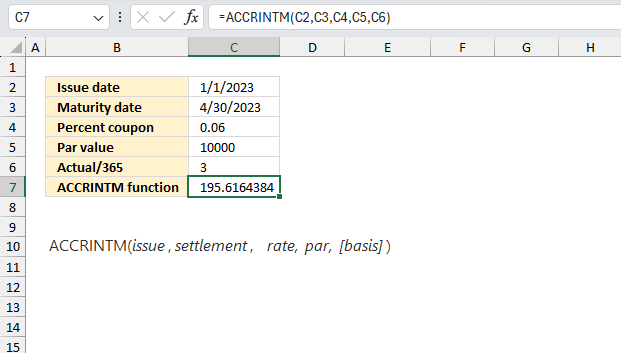
A bond with a par value of $10,000 and an annual coupon rate of 6% was issued on January 1, 2023. Calculate the accrued interest for the period from January 1, 2023, to April 30, 2023?
The arguments are:
| Issue date | 1/1/2023 |
| Maturity date | 4/30/2023 |
| Percent coupon | 0.06 |
| Par value | 10000 |
| Actual/365 | 3 |
| ACCRINTM function | 195.62 |
Formula in cell C7:
The formula returns 195.62 in cell C7.
The ACCRINTM function calculates the accrued interest for a security that pays interest at maturity using the following formula:
ACCRINTM = par × rate × (A / D)
Lets check if we can calculate the result manually, we have:
par = $10,000
rate = 0.06 (6% annual coupon rate)
A = 120 (the number of days from January 1, 2023, to April 30, 2023)
D = 365 (assuming an actual/365 day-count convention)
Plugging these values into the formula:
ACCRINTM = par × rate × (A / D)
$10,000 × 0.06 × (119 / 365) = 195.62
The accrued interest for the bond from January 1, 2023, to April 30, 2023 is $195.62
4. Example 2
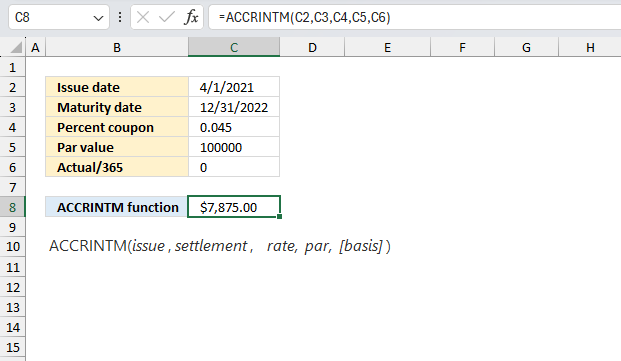
A company issued a 5-year bond with a par value of $100,000 and an annual coupon rate of 4.5% on April 1, 2021. The bond pays interest at maturity. Calculate the accrued interest for the period from April 1, 2021, to December 31, 2022?
The arguments are:
| Issue date | 4/1/2021 |
| Maturity date | 12/31/2022 |
| Percent coupon | 0.045 |
| Par value | 100000 |
| Actual/365 | 0 |
Formula in cell C8:
The formula returns $7,875.00 in cell C8.
The ACCRINTM function calculates the accrued interest for a security that pays interest at maturity using the following formula:
ACCRINTM = par × rate × (A / D)
Lets check if we can calculate the result manually, we have:
par = $100,000
rate = 0.045 (4.5% annual coupon rate)
A = 639 (the number of days from April 1, 2021, to December 31, 2022)
D = US (NASD) 30/360
Plugging these values into the formula:
ACCRINTM = par × rate × (A / D)
$100,000 × 0.045 × (639/ 360) = 7987.5
The accrued interest for the bond from April 1, 2021, to December 31, 2022 is $7987.5
This value is not equal to the calculated value in cell C8. It looks like [basis] = 0 (zero) makes the formula use 365 day count or I have made a mistake somewhere in the calculations.
5. Example 3
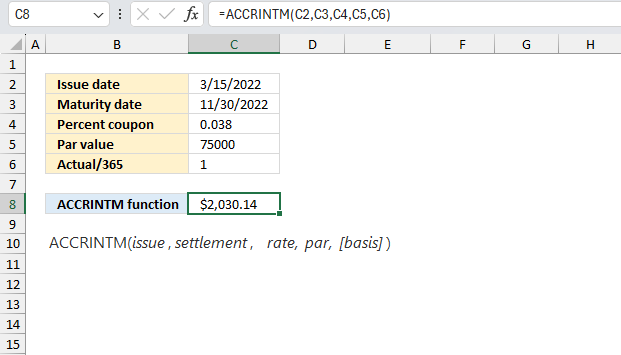
A bond with a par value of $75,000 and an annual coupon rate of 3.8% was issued on March 15, 2022. The bond pays interest at maturity. Calculate the accrued interest for the period from March 15, 2022, to November 30, 2022?
The arguments are:
| Issue date | 3/15/2022 |
| Maturity date | 11/30/2022 |
| Percent coupon | 0.038 |
| Par value | 75000 |
| Actual/365 | 1 |
Formula in cell C8:
The formula returns $2,030.14 in cell C8.
The ACCRINTM function calculates the accrued interest for a security that pays interest at maturity using the following formula:
ACCRINTM = par × rate × (A / D)
Lets check if we can calculate the result manually, we have:
par = $75,000
rate = 0.038 (3.8% annual coupon rate)
A = 260 (the number of days from April 1, 2021, to December 31, 2022)
D = 365
Plugging these values into the formula:
ACCRINTM = par × rate × (A / D)
$75,000 × 0.038 × (260/ 365) = 2,030.137
The accrued interest for the bond from 3/15/2022, to 11/30/2022 is $2,030.137
Functions in 'Financial' category
The ACCRINTM function function is one of 27 functions in the 'Financial' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form