How to use the IPMT function
What is the IPMT function?
The IPMT function calculates the interest payment for a specific period for an investment based on repeated constant payments and a constant interest rate.
IPMT stands for Interest Payment, reflecting that the function isolates just the interest portion of a periodic payment calculation based on an interest rate, periods, PV, FV, etc.
1. Introduction
What is interest payment?
An interest payment is the amount of interest owed or earned on a loan or investment for a specific payment period. The IPMT function calculates the interest portion of a periodic payment on an investment or loan. Interest payments decline over time as the principal is paid off.
What is an investment?
An investment is the purchase of an asset with the expectation of generating income or appreciation in the future. For example, stocks, bonds, real estate, commodities, art etc.
What are periodic constant payments?
Periodic constant payments are payments that are made at regular intervals such as monthly, quarterly, or yearly and have the same amount each time.
What is a constant interest rate?
A fixed interest rate is an interest rate that remains the same throughout the term of a loan or an investment.
What is the principal?
The principal is the amount you have to pay back and interest is the charges you pay for borrowing the money.
What is the difference between the IPMT function and the ISPMT function?
The IPMT function lets you also specify a future value [fv] and when the payments are due [type] which is not the case with the ISPMT function.
ISPMT(rate, per, nper, pv)
IPMT(rate, per, nper, pv, [fv], [type])
IPMT function is commonly used for loans where the repayment schedule involves even periodic payments.
The ISPMT function calculates the interest payment for a given period in an investment or loan with even principal payments.
2. IPMT function Syntax
IPMT(rate, per, nper, pv, [fv], [type])
| rate | Required. The interest rate. |
| per | Required. The period. |
| nper | Required. The total number of periods in an annuity.
Examples: |
| pv | Required. Present value. |
| [fv] | Optional. Future value, default value is 0 (zero). |
| [type] | Optional. When payments are due.
0 - End of period, default value. |
3. IPMT Function Example 1
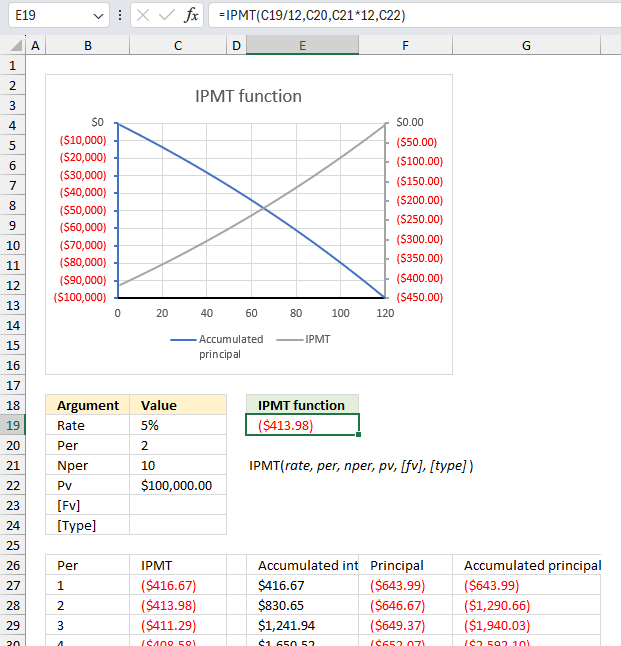
You took out a $100,000 mortgage loan at 5% annual interest rate for 10 years. What is the interest payment for the 2nd month of the loan?
The arguments for the IPMT function are :
- Rate: This is the interest rate per period. In the example, it is set to 5%.
- Per: This is the period for which the interest payment is calculated. In the example, it is set to 2 which corresponds to the 2nd month.
- Nper: This is the total number of periods for the loan or investment. In the example, it is set to 10 years. We will convert this to months in the formula by multiplying 10 by 12 which equals 120.
- Pv: This is the present value or the initial loan amount. In the example, it is set to $100,000.00.
- [fv] (optional): This is the future value or the remaining balance after the last payment. In the example, it is left blank, assuming a future value of 0 (the loan is fully paid off).
- [Type] (optional): This is the timing of the payments (0 for payments due at the end of the period, 1 for payments due at the beginning of the period). In the example, it is left blank, assuming the default end-of-period payment.
Formula in cell E3:
The output of the IPMT function, based on the given arguments, is ($413.98), which represents the interest payment for the second period (Per = 2) of the loan. Use the same unit for rate and nper, the above example uses monthly payments. That is why the interest rate is divided by 12 and nper is multiplied by 12. There are 120 monthly payments in a 10 year period.
The table below the chart and input arguments shows the calculation details for each period, including the period number (Per), interest payment (IPMT), accumulated interest, principal payment, and accumulated principal.
The image shows the use of the IPMT function in Excel to calculate the interest payment for a given period of a loan or investment. It also shows how the interest payment relates to the accumulated principal and the remaining loan balance over time.
The chart titled "IPMT function" displays a line graph with two lines. The blue line represents the accumulated principal, which starts at 0 and increases over time as payments are made and ends with 100,000 which corresponds to the present value (pv) in cell C22. The blue line uses the left y-axis which is also blue in color.
The orange line represents the IPMT (interest payment) for each period, which starts high and decreases over time as the principal is paid down. The gray line uses the right y-axis which is also gray in color.
4. IPMT Function Example 2

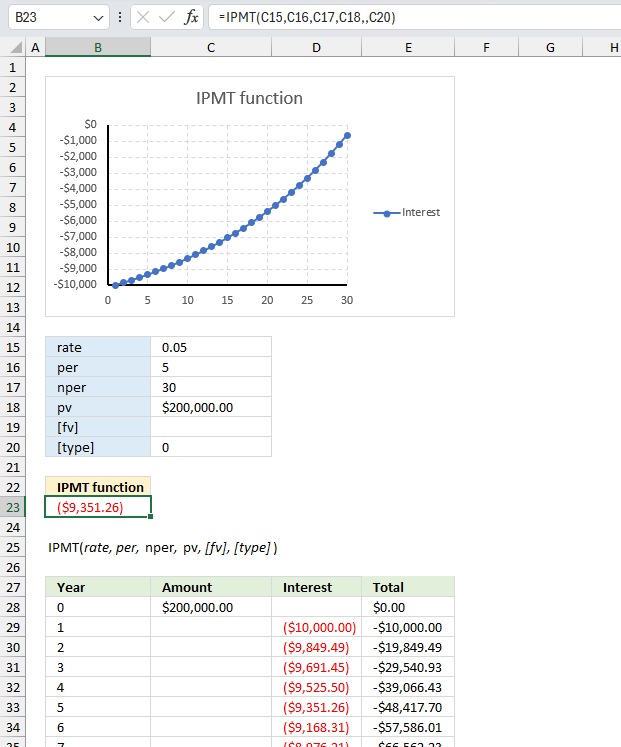
You took out a $200,000 mortgage loan at 5% annual interest rate for 30 years. What is the interest payment for the 5th year of the loan?
The arguments for the IPMT function are :
- Rate: This is the interest rate per period. In the example, it is set to 5%.
- Per: This is the period for which the interest payment is calculated. In the example, it is set to 5 which corresponds to the 5th year.
- Nper: This is the total number of periods for the loan or investment. In the example, it is set to 30 years.
- Pv: This is the present value or the initial loan amount. In the example, it is set to $200,000.00.
- [fv] (optional): This is the future value or the remaining balance after the last payment. In the example, it is left blank, assuming a future value of 0 (the loan is fully paid off).
- [Type] (optional): 0 This is the timing of the payments (0 for payments due at the end of the period, 1 for payments due at the beginning of the period). If left blank, assuming the default end-of-period payment.
The result displayed is ($9,351.26), which is the interest payment for the 5th period based on these inputs. The chart shows the interest payment for each period represented by the blue curve. It starts from 10,000 and decreases over time as the remaining principal decreases. The x axis shows the the period starting from 0 to 30, the periods represents the years in this example.
Functions in 'Financial' category
The IPMT function function is one of 27 functions in the 'Financial' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form