How to use the ASINH function
What is the ASINH function?
The ASINH function calculates the inverse hyperbolic sine of a number.
What is the SINE function?
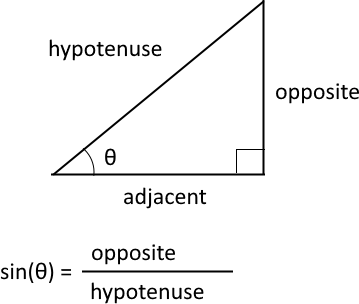
The sine is a trigonometric function that relates an angle θ in a right triangle to the ratio of the length of the side opposite the angle and the length of the longest side (hypotenuse) of the triangle. A right triangle has one angle that measures 90° or π/2 radians which is approximately 1.5707963267949 radians.
The SIN function calculates the ratio between the opposite side and the hypotenuse.
What is the hyperbolic sine?
The hyperbolic sine, abbreviated as sinh, is one of the main hyperbolic functions.
Hyperbolic sine is defined as:
sinh(x) = (e^x - e^-x) / 2
What is the difference between the hyperbolic sine and the trigonometric sine?
The differences between sinh and the regular trigonometric sine is that regular sine is defined in terms of angles on the unit circle while the sinh function is defined in terms of exponential functions. Sine relates to circles, sinh relates to hyperbolas.
Sine is defined in terms of angles on the unit circle and is periodic repeating every 2π radians. The hyperbolic sine is not repeating. Sine takes an angle as input while the sinh takes a real number. Sine has values between -1 and 1 in contrast to the sinh which is undefined.
What is hyperbolic/hyperbolas?
Hyperbolic functions are similar to ordinary trigonometric functions, but they use a different shape to define them called hyperbolas.
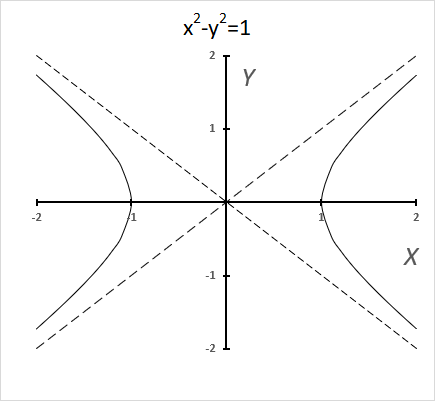
The chart above shows a hyperbola and two asymptotes (dashed lines) where the intersection is at the center of the hyperbola.
The unit hyperbola looks like this:
It shows x2 -y2=1 and x2 -y2=-1
What is the inverse hyperbolic sine?
It calculates the hyperbolic value x which would be the angle θ in terms of trigonometric functions. However, the hyperbolic value is not an angle but a real number.
arcsinh(x) = ln(x + √(x2 + 1))
What are the asymptotes for the inverse hyperbolic sine?
Asymptotes refer to a straight lines that the function approaches but never reaches. The inverse hyperbolic sine function, asinh(x), has a horizontal asymptote at y = 0
What is LN?
LN is the natural logarithm, e is the base to the natural logarithm.
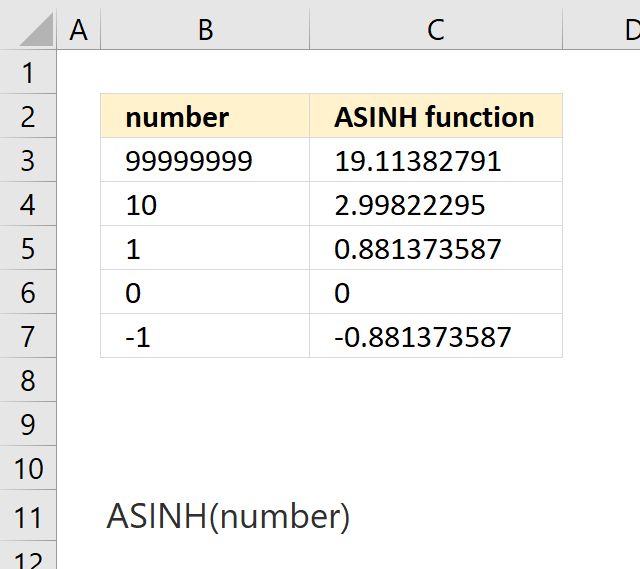
Excel Function Syntax
ASINH(number)
Arguments
| number | Required. Any real number. |
=ASINH(B3)
Comments
The inverse hyperbolic sine is the value whose hyperbolic sine is number, so ASINH(SINH(number)) equals number.
Useful links
ASINH function - Microsoft
Graphs of Hyperbolic Functions
Functions in 'Math and trigonometry' category
The ASINH function function is one of 73 functions in the 'Math and trigonometry' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form