What is the SERIESSUM function?

The SERIESSUM function calculates the sum of a power series based on the following formula:

SERIESSUM(x, n, m, a) = a₁xⁿ + a₂x^^(n+m)+a₃x^{(n+2m) + ... +} a_ix^(n+(i-1)m)

This allows you to approximate a mathematical function by a power series expansion.

What is a power series expansion?

A power series expansion expresses a function as an infinite series of terms with progressively higher power. It can be used to approximate functions.

What is the purpose of approximate functions?

Approximations trade off accuracy for simplicity in order to make calculations faster and to make calculations easier. Many important functions like sine, cosine, exponentials, and so on. are difficult to compute directly, approximating them with polynomials or series expansions made computation easier before electronics.

What are polynomials?

A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents.

Polynomials can have one or more variables: 4x² + 3xy - 7y³

SERIESSUM Function Syntax

SERIESSUM(x, n, m, coefficients)

SERIESSUM Function Arguments

x	Required. The input value to the power series.
n	Required. The initial power to which you want to raise x.
m	Required. The step by which to increase n for each term in the series.
coefficients	Required. A set of coefficients by which each successive power of x is multiplied. The number of values in coefficients determines the number of terms in the power series. For example, if there are three values in coefficients, then there will be three terms in the power series.

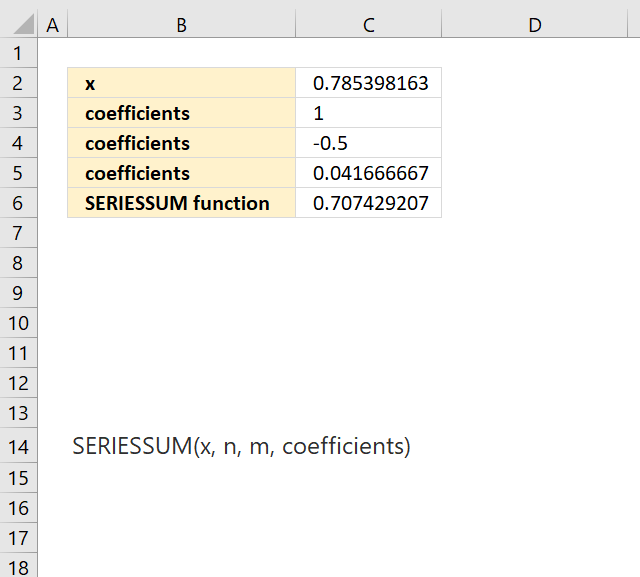
SERIESSUM function example 1

The Maclaurin series for cosine is:

cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...

Formula in cell C6:

Formula in cell C2:

=PI()/4

Formula in cell C3:

=1

Formula in cell C4:

=-1/FACT(2)

Formula in cell C5:

=1/FACT(4)

An approximation to the cosine of Pi/4 radians, or 45 degrees (0.707103).

SERIESSUM function example 2

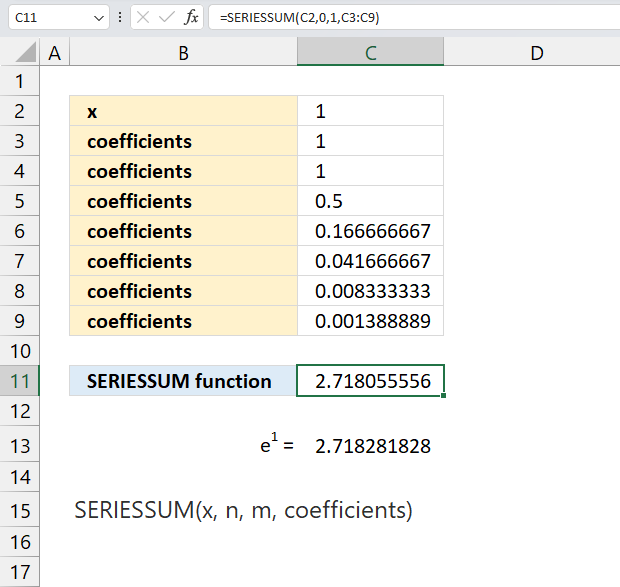
Here is a simple example to demonstrate using the SERIESSUM function in Excel for learning purposes:

Let's approximate e^x using its Taylor series expansion:

e^x = 1 + x + x^2/2! + x^3/3! + ...

x is specified in cell C2 and it contains 1.

e^x = 1 + x + x^2/2! + x^3/3! + ...

becomes

1 + 1 + 1²/2! + 1³/3! + 1⁴/4! + 1⁵/5! + 1⁶/6!

becomes

1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + 1/720

Formula in cell C11:

=SERIESSUM(C2,0,1,C3:C9)

 

Functions in 'Math and trigonometry' category

The SERIESSUM function function is one of many functions in the 'Math and trigonometry' category.

Excel function categories

Excel categories

Leave a Comment