How to use the SECH function
What is the SECH function?
The SECH function calculates the hyperbolic secant of an angle.
What is a secant?
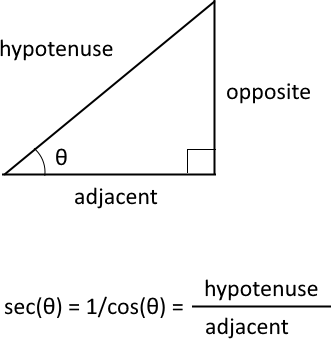
The trigonometric secant is a function that defines an angle of a right-angled triangle to the ratio of the hypotenuse to the adjacent side. It is also the inverse of the cosine, sec(θ) = 1/cos(θ).
Trigonometric functions are defined on the unit circle and deal with angles, circular geometry, however, hyperbolic functions are defined on the unit hyperbola and deal with hyperbolas, hyperbolic geometry.
What is a hyperbolic secant?
The hyperbolic secant is a trigonometric function defined as:
sech(x) = 1/cosh(x)
Where cosh(x) is the hyperbolic cosine function.
It is the reciprocal or inverse of the hyperbolic cosine function, just as the regular secant is 1/cos(x). The graph of y = sech(x) forms a S-shape, asymptotic to y = 0 as x approaches ±infinity.
sech(x) is an even function, with sech(-x) = sech(x). It has a vertical asymptote at 0 and no horizontal asymptotes. Hyperbolic functions are analogs of trigonometric functions for hyperbolas rather than circles.
What is a hyperbole?
Hyperbolic functions are similar to ordinary trigonometric functions, but they use a different shape to define them called hyperbolas.
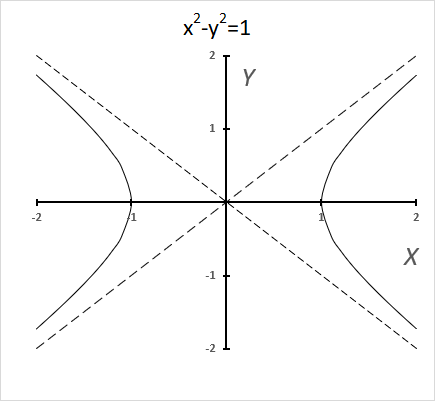
The chart above shows a hyperbola and two asymptotes (dashed lines) where the intersection is at the center of the hyperbola.
The unit hyperbola looks like this:
x2 -y2=1 and x2 -y2=-1
These functions get closer, however, they never crosses or touches these dashed lines (asymptotes).
What are the hyperbolic secant asymptotes?
The hyperbolic secant function (sech(x)) has two vertical asymptotes located at x = 0 and x = ±∞
This means that as x approaches 0 from either side, sech(x) approaches ±∞ and as x approaches positive or negative infinity, sech(x) approaches 0
What are the main hyperbolic functions, their domain and range?
| Hyperbolic | Domain | Range |
| sinh(x) | All real numbers | (-∞, ∞) |
| cosh(x) | All real numbers | [1, ∞) |
| tanh(x) | All real numbers | (-1, 1) |
| sech(x) | All real numbers | (0, 1) |
What is the hyperbolic domain?
The domain of a hyperbolic function refers to the set of input values it is defined and valid for.
What is the hyperbolic range?
The range of a hyperbolic function refers to the set of possible output values it returns.
| Hyperbolic Function | Formula | Asymptotes |
| sinh | sinh x = (e^x - e^-x)/2 | y = e^x/2 and y = -e^-x/2 |
| cosh | cosh x = (e^x + e^-x)/2 | y = 0 and y = ∞ |
| tanh | tanh x = (e^x - e^-x)/(e^x + e^-x) | y = -1 and y = 1 |
| coth | coth x = (e^x + e^-x)/(e^x - e^-x) | x = nπ and y = -1 and y = 1 |
| sech | sech x = 2/(e^x + e^-x) | y = 0 and y = ∞ |
| csch | csch x = 2/(e^x - e^-x) | x = nπ and y = 0 and y = ∞ |
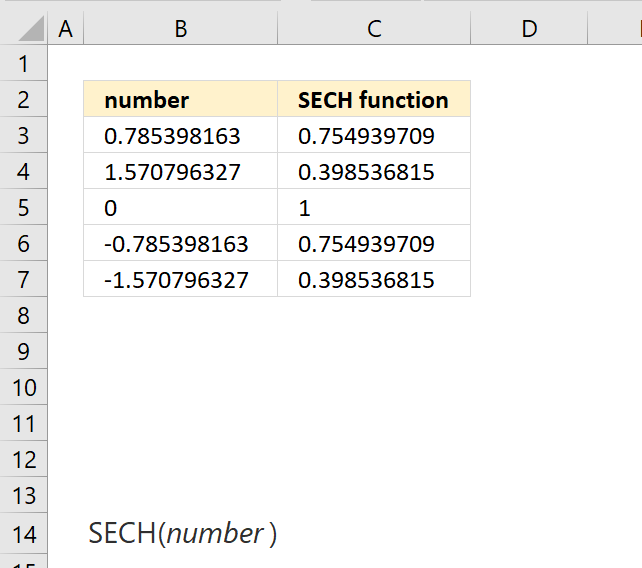
Formula in cell C3:
Excel Function Syntax
SECH(number)
Arguments
| number | Required. An angle in radians. |
Comments
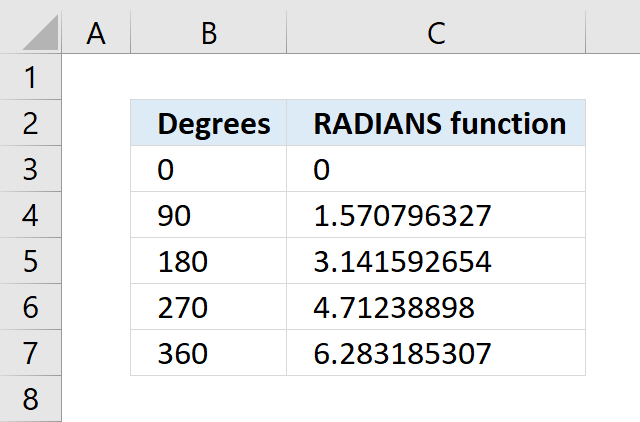
Use the RADIANS function to convert degrees to radians.
Recommended articles
What is the RADIANS function? The RADIANS function converts degrees to radians. What is radian? Radians measure angles by the […]
Functions in 'Math and trigonometry' category
The SECH function function is one of 73 functions in the 'Math and trigonometry' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form