How to use the SINH function
What is the SINH function?
The SINH function calculates the hyperbolic sine of a number.
What is the hyperbolic sine of a number?
The sinh functions models hyperbolic geometry and is used in differential equations, statistics, physics, and engineering.
sinh(x) = (e^x - e^-x) / 2
or
sinh(x) = tanh(x) * cosh(x)
The input x can be any real number, unlike the regular sine function which takes angles in radians. e is approximately equal to 2.71828.
What is the difference between the hyperbolic sine and the trigonometric sine?
sinh(x) takes a real number x as input while sin(θ) takes an angle θ in radians. The sine curve repeats every 2π radians, whereas sinh(x) asymptotes to ±∞ without repeating. sin(θ) ranges from -1 to 1 as output while sinh(x) spans all real numbers.
What is hyperbolic?
Hyperbolic functions are similar to ordinary trigonometric functions, but they use a different shape to define them.
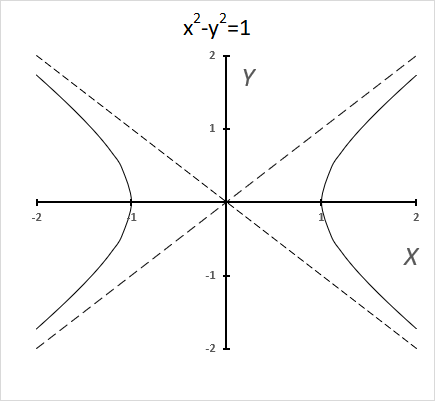
Trigonometric functions use a circle, while hyperbolic functions use hyperbolas. The chart above shows a hyperbola and two asymptotes (dashed lines) where the intersection is at the center of the hyperbola.
The unit hyperbola looks like this:
It shows x2 -y2=1 and x2 -y2=-1
What are asymptotes?
Asymptotes are straight lines that the function curves towards but never intersects.
What are the domain, range and asymptotes of all the main hyperbolic functions?
This table displays the key properties of the main hyperbolic functions:
| Hyperbolic Function | Domain | Asymptotes | Range |
| sinh(x) | All real numbers | Vertical asymptotes at multiples of ±πi/2 | (-∞, ∞) |
| cosh(x) | All real numbers | Horizontal asymptotes at y=0 | (1, ∞) |
| tanh(x) | All real numbers | Horizontal asymptotes at y=±1 | (-1, 1) |
| sech(x) | All real numbers | Horizontal asymptotes at y=0 | (0, 1) |
| csch(x) | All real x ≠ 0 | Vertical asymptotes at x=0 | (0, ∞) |
| coth(x) | All real numbers | Horizontal asymptotes at y=±1 | (1, ∞) |
The asymptotes shows the exponential nature and infinite limits of hyperbolic functions.
What are the domain, range and asymptotes of all the main inverse hyperbolic functions?
This table displays the key properties of the inverse hyperbolic functions:
| Inverse Hyperbolic Function | Domain | Asymptotes | Range |
| arcsinh(x) | All real numbers | Horizontal asymptote at y=0 | (-∞, ∞) |
| arccosh(x) | x>=1 | None | (0, ∞) |
| arctanh(x) | -1<x<1 | Vertical asymptotes at x=±1 | (-∞, ∞) |
| arcsech(x) | 0<x<1 | None | (0, ∞) |
| arccsch(x) | All real x ≠ 0 | Vertical asymptote at x=0 | (-∞, ∞) |
| arccoth(x) | All real numbers | None | (0, ∞) |
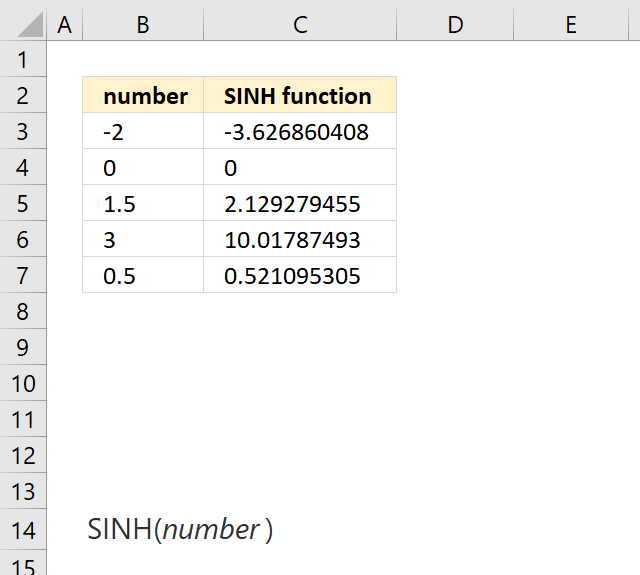
Formula in cell C3:
Excel Function Syntax
SINH(number)
Arguments
| number | Required. Any real number. |
Comments
SINH(n) = (EXP(n)-EXP(-n))/2
Recommended articles
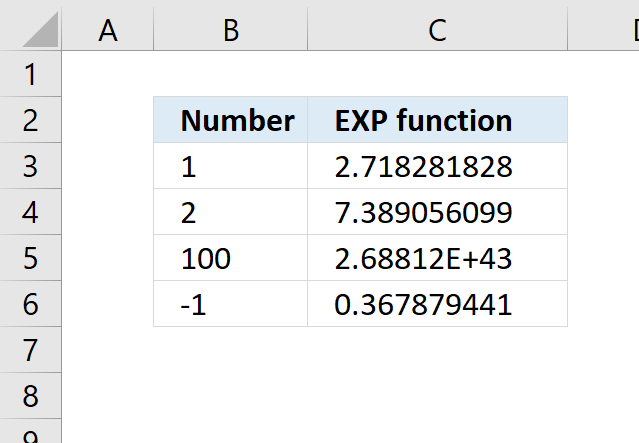
What is the EXP function? The EXP function returns e raised to the power of a given number. Table of […]
SINH(n) = TANH(n)*COSH(n)
Functions in 'Math and trigonometry' category
The SINH function function is one of 73 functions in the 'Math and trigonometry' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form