How to use the COSH function
What is the COSH function?
The COSH function calculates the hyperbolic cosine of a number.
What is the hyperbolic cosine of a number?
The hyperbolic cosine is a hyperbolic function defined as:
cosh(x) = (e^x + e^-x)/2
What is e?
The number e is an irrational constant that is approximately equal to 2.71828. It is the base of the natural logarithm function, which is denoted by ln. The natural logarithm function is the inverse of the natural exponential function, which is denoted by ex. This means that if y = ex, then x = ln y.
What is a hyperbole?
Hyperbolic functions are similar to ordinary trigonometric functions, but they use a different shape to define them called hyperbolas.
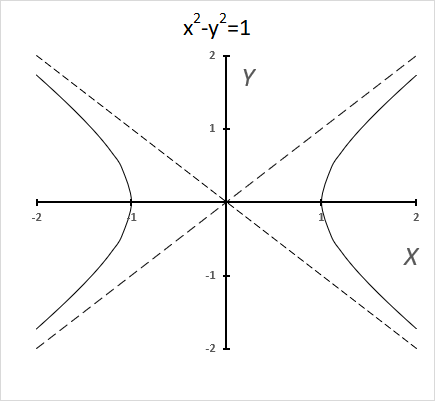
The chart above shows a hyperbola and two asymptotes (dashed lines) where the intersection is at the center of the hyperbola.
The unit hyperbola looks like this:
It shows x2 -y2=1 and x2 -y2=-1
These functions get closer, however, they never crosses or touches these dashed lines (asymptotes).
What are the hyperbolic cosine asymptotes?
The asymptotes of the hyperbolic cosine function are the lines:
- y = +∞
- y = -∞,
This means that the function never crosses or touches these lines, but gets closer and closer to them as x goes to +infinity or -infinity.
What are the main hyperbolic functions, their domain and range?
| Hyperbolic | Domain | Range |
| sinh(x) | All real numbers | (-∞, ∞) |
| cosh(x) | All real numbers | [1, ∞) |
| tanh(x) | All real numbers | (-1, 1) |
| sech(x) | All real numbers | (0, 1) |
What is the hyperbolic domain?
The domain of a hyperbolic function refers to the set of input values it is defined and valid for.
What is the hyperbolic range?
The range of a hyperbolic function refers to the set of possible output values it returns.
| Hyperbolic Function | Formula | Asymptotes |
| sinh | sinh x = (e^x - e^-x)/2 | y = e^x/2 and y = -e^-x/2 |
| cosh | cosh x = (e^x + e^-x)/2 | y = 0 and y = ∞ |
| tanh | tanh x = (e^x - e^-x)/(e^x + e^-x) | y = -1 and y = 1 |
| coth | coth x = (e^x + e^-x)/(e^x - e^-x) | x = nπ and y = -1 and y = 1 |
| sech | sech x = 2/(e^x + e^-x) | y = 0 and y = ∞ |
| csch | csch x = 2/(e^x - e^-x) | x = nπ and y = 0 and y = ∞ |
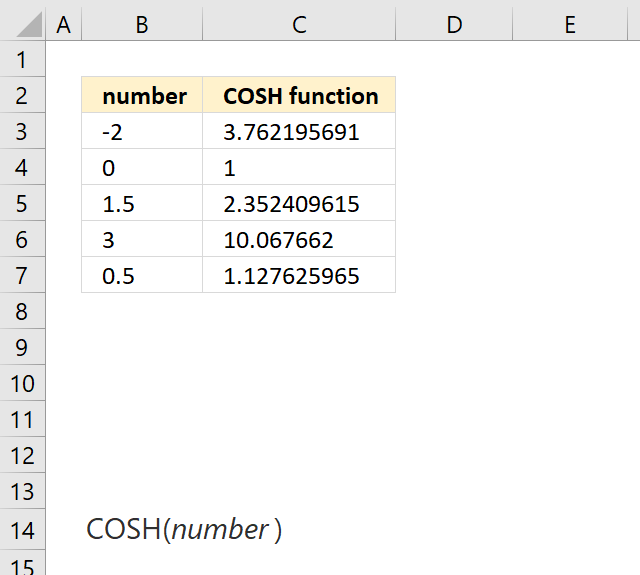
1. COSH function Syntax
COSH(number)
2. COSH function Arguments
| number | Required. Any real number. |
Comments
COSH(n) = (EXP(n)+EXP(-n))/2
Recommended articles
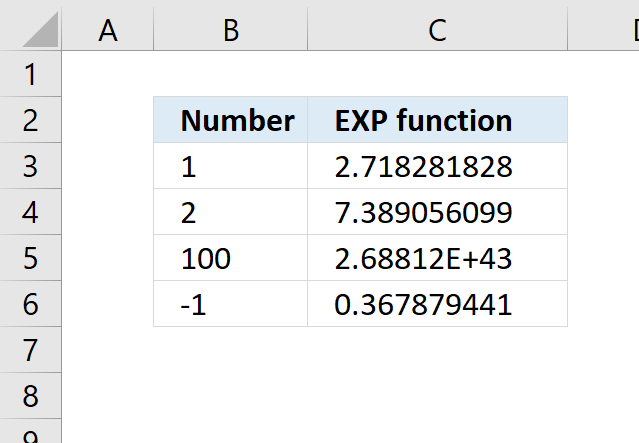
What is the EXP function? The EXP function returns e raised to the power of a given number. Table of […]
3. COSH function example
Formula in cell C3:
Functions in 'Math and trigonometry' category
The COSH function function is one of 73 functions in the 'Math and trigonometry' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form