How to use the FORECAST.LINEAR function
What is the FORECAST.LINEAR function?
The FORECAST.LINEAR function calculates a value based on existing x and y values using linear regression. Use this function to predict linear trends.
FORECAST.LINEAR replaced the FORECAST function in Excel 2016.
Table of Contents
1. Introduction
When to predict linear trends?
The data shows an approximately linear relationship between the variables. A scatterplot can be used to visualize this.
The FORECAST.LINEAR function is great for extrapolating a trend beyond the observed data. A linear equation provides a simple method for predicting linear trends.
What is a linear equation?
A linear equation is a type of equation that can be written in the form ax + b = 0, where a and b are constants and x is a variable. A linear equation represents a relationship between two quantities that are proportional to each other.
For example, if you have a linear equation that says y = 3x + 4, it means that for every unit increase in x, the value of y increases by 3 units and when x is zero y is 4.
The graph of a linear equation is always a straight line, a linear equation does not involve powers of variables.
Related functions to linear trends
| Function | Description |
|---|---|
| LINEST(known_y's, [known_x's], [const], [stats]) | Returns statistics for a linear trend line fit to data |
| GROWTH(known_y's, [known_x's], [new_x's], [const]) | Returns predicted y-values for exponential growth trend |
| TREND(known_y's, [known_x's], [new_x's], [const]) | Calculates values along a linear trend |
2. FORECAST.LINEAR Function Syntax
FORECAST.LINEAR(x, known_y's, known_x's)
3. FORECAST.LINEAR Function Arguments
| x | Required. The data point for which you want to predict a value. |
| known_y's | Required. Known y points. |
| known_x's | Required. Known x points. |
4. FORECAST.LINEAR Function Example 1

You have monthly sales data for the past three years and want to forecast the sales for the next six months. Use the FORECAST.LINEAR function to predict the future sales based on the historical data?
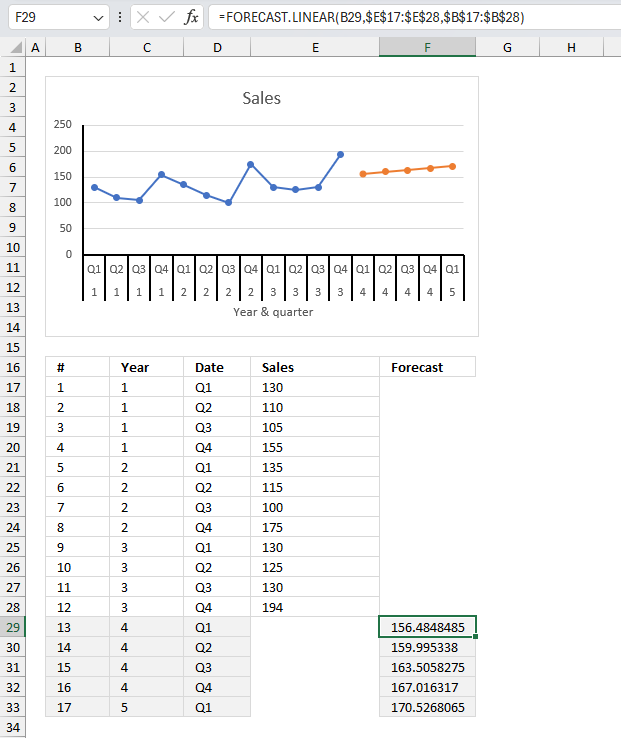
The image above shows the sales data for the last three years in cell range C17:E28, here is the data:
| # | Year | Date | Sales |
| 1 | 1 | Q1 | 130 |
| 2 | 1 | Q2 | 110 |
| 3 | 1 | Q3 | 105 |
| 4 | 1 | Q4 | 155 |
| 5 | 2 | Q1 | 135 |
| 6 | 2 | Q2 | 115 |
| 7 | 2 | Q3 | 100 |
| 8 | 2 | Q4 | 175 |
| 9 | 3 | Q1 | 130 |
| 10 | 3 | Q2 | 125 |
| 11 | 3 | Q3 | 130 |
| 12 | 3 | Q4 | 194 |
The arguments for the FORECAST.LINEAR function are:
FORECAST.LINEAR(x, known_y's, known_x's)
- x - B29
- known_y's - $E$17:$E$28
The dollar signs lets you lock the cell reference to E17:E28. This means that when we copy cell F29 to cells below this cell reference stays the same. This makes sure that the same historical data is used for each new future value we calculate.
- known_x's - $B$17:$B$28
The dollar signs lets you lock the cell reference to B17:B28. This means that when we copy cell F29 to cells below this cell reference stays the same. This makes sure that the same historical data is used for each new future value we calculate.
The formula in cell F29 calculates the future sales value for quarter 1 based on the historical data in $E$17:$E$28 and $B$17:$B$28
Formula in cell F29:
Cell F29 is copied to cells below as far as needed. The chart above shows the future values as a orange line, the blue line represents historical sales data specified in cell range E17:E28 and B17:B28.
The chart above is a line chart with two different series, the first serie is in $E$17:$E$33 and the second serie is in $F$17:$F$33. Both series share the same x values.
Sales data often show non-linear patterns due to various factors such as seasonality, market trends, economic conditions, and consumer behavior etc. A linear function assumes a constant rate of change, which may not accurately capture the underlying patterns and dynamics of sales data.
5. FORECAST.LINEAR Function Example 2
A geologist has collected geological data for the past decade and wants to forecast the next years. Use the FORECAST.LINEAR function to estimate future data based on the given data?
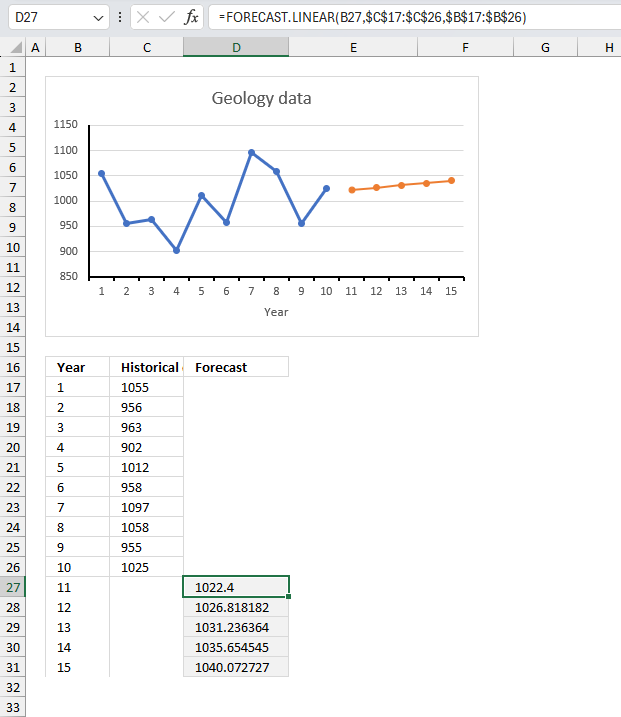
The image above shows the sales data for the last decade in cell range C17:C26, here is the data:
| Year | Historical data |
| 1 | 1055 |
| 2 | 956 |
| 3 | 963 |
| 4 | 902 |
| 5 | 1012 |
| 6 | 958 |
| 7 | 1097 |
| 8 | 1058 |
| 9 | 955 |
| 10 | 1025 |
The arguments for the FORECAST.LINEAR function are:
FORECAST.LINEAR(x, known_y's, known_x's)
- x - B27
- known_y's - $C$17:$C$26
The dollar signs lets you lock the cell reference to C17:C26. This means that when we copy cell D27 to cells below this cell reference stays the same. This makes sure that the same historical data is used for each new future value we calculate.
- known_x's - $B$17:$B$26
The dollar signs lets you lock the cell reference to B17:B26. This means that when we copy cell D27 to cells below this cell reference stays the same. This makes sure that the same historical data is used for each new future value we calculate.
The formula in cell F29 calculates the future geological value for year 11 based on the historical data in C17:C26 and B17:B26. The orange line displaying the future values in the image appears as a straight line reflecting the linear nature of the regression model used for the prediction.
Formula in cell D27:
Cell D27 is copied to cells below as far as needed.
6. FORECAST.LINEAR function not working
FORECAST.LINEAR function returns a
- #VALUE error if x is not numeric.
- #N/A error if known_y's or known_x's is left out.
- #DIV/0! error value if the variance of known_x's evaluates to zero.
7. What is the math formula behind the FORECAST.LINEAR function
a = ȳ - bx̄
The expression a = ȳ - bx̄ represents the equation for the y-intercept (a) of the linear regression line, where:
- ȳ is the mean or average value of the dependent variable y.
- b is the slope of the linear regression line.
- x̄ is the mean or average value of the independent variable x.
b = Σ(x - x̄)(y - ȳ)/Σ(x - x̄)2
Formula b represents the slope of the linear regression line which is used to model the linear relationship between two variables, x and y.
Σ(x - x̄)(y - ȳ) calculates the sum of the products of the deviations of x from its mean (x̄) and the deviations of y from its mean (ȳ) for each data point (x, y). It measures the covariance between the variables x and y.
Σ(x - x̄)2 calculates the sum of the squared deviations of x from its mean (x̄). It represents the variance of the x values.
Dividing Σ(x - x̄)(y - ȳ) by Σ(x - x̄)2 gives the slope of the linear regression line, which describes the change in the mean value of y for a unit change in x.
Functions in 'Statistical' category
The FORECAST.LINEAR function function is one of 73 functions in the 'Statistical' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form