How to use the PERMUTATIONA function
What is the PERMUTATIONA function?
The PERMUTATIONA function returns the number of permutations for a specific number of elements that can be selected from a larger group of elements. Repetition is allowed.
Table of Contents
1. Introduction
Explain what a permutation is?
A permutation is a way of arranging a set of elements in a specific order. For example, if you have three letters A, B, and C, you can arrange them in six different ways: ABC, ACB, BAC, BCA, CAB, and CBA.
Each of these arrangements is called a permutation of the three letters. The order of the objects matters in a permutation, so ABC and BAC are considered different permutations.
What is repetition allowed?
Repetition allowed is when there can be duplicate values. A phone number is a great example of a permutation that may contain duplicate digits.
What is an element?
An element refers to an item which can be anything.
What is the difference between the PERMUTATIONA function and the PERMUT function?
PERMUTATIONA allows repetition, PERMUT does not.
PERMUTATIONA calculates the number of permutations for a given number of objects (n) selected from a pool of objects where order is important and objects can repeat.
PERMUT calculates the number of permutations for a given number of objects (n) selected from a pool of unique objects where order is important but repetition is not allowed.
How can I create a list of permutations with repetition?
Recommended articles
This blog post demonstrates a custom function (UDF) that creates permutations. Repetition is allowed. The custom function lets you specify the […]
What is the difference between combination and permutation?
Combinations: Order does not matter. ABC and BAC are considered the same.
Permutations - Order matters. ABC is different from BAC.
Permutations are used when order matters - like sequences, orders, arrangements.
Combinations are used when specific groupings matter but order doesn't - like teams, packs, sets.
How can I create a list of permutations without repetition?
Recommended articles
This blog post describes how to create permutations, repetition is NOT allowed. Permutations are items arranged in a given order meaning […]
Related functions
| Excel Function and Arguments | Description |
|---|---|
| PERMUT(number, number_chosen) | Returns the number of permutations for a given number of objects selected from number items without repetition |
| PERMUTATIONA(number, number_chosen) | Returns the number of permutations for a given number of objects selected from number items with repetition allowed |
| COMBIN(number, number_chosen) | Returns the number of combinations for a given number of objects selected from number items without repetition |
| COMBINA(number, number_chosen) | Returns the number of combinations for a given number of objects selected from number items with repetition allowed |
2. Syntax
PERMUTATIONA(number, number-chosen)
3. Arguments
| number | The total number of elements. |
| number-chosen | A specific number of elements. |
4. Example
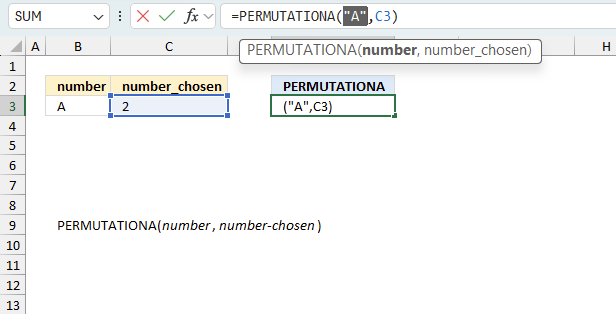
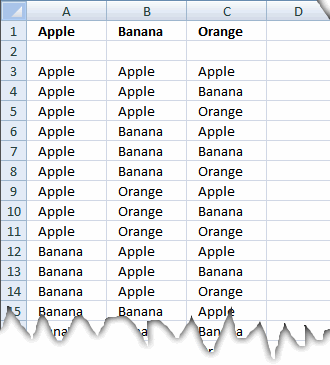
A jewelry designer is creating a new bracelet design with two different gemstones. The available gemstones are ruby, emerald, and sapphire. If the order of the gemstones matters and repetition is allowed, how many different bracelet designs can be created?
The picture above shows permutations with repetition allowed, 2 out of 3 gemstones.
Formula in cell D3:
The formula returns 9 different bracelet designs can be created.
5. Create a list of permutations - Excel 365
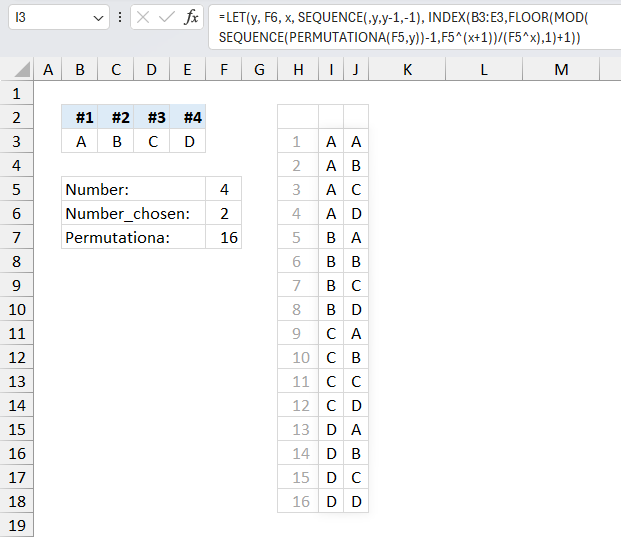
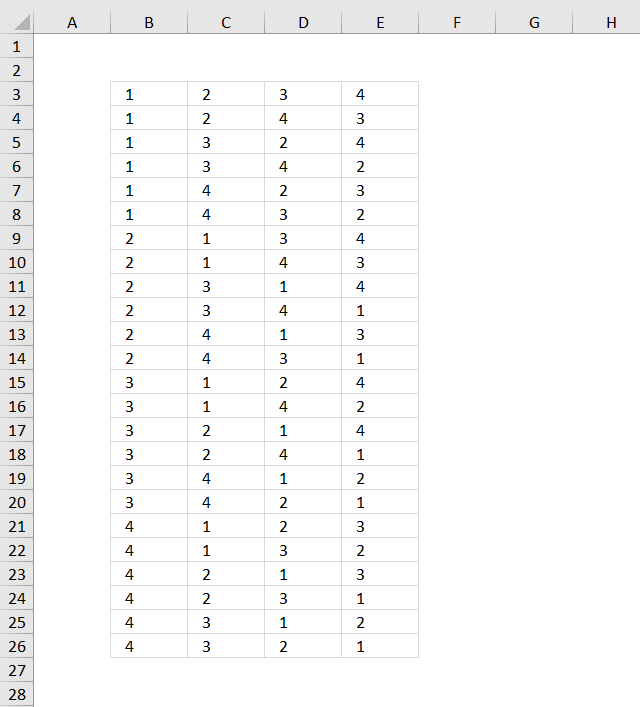
A manufacturing company has four different types of metals available (A, B, C, and D), repetition is allowed. They want to explore various permutations by arranging two metals together. The goal is to determine all the possible arrangements or permutations that can be formed by selecting two metals at a time from the four available options.
To calculate the number of permutations and list them out, we can use the following approach:
Total number of metals = 4
Number of metals to be selected for each arrangement = 2
We can use the PERMUT function to calculate the number of permutations:
=PERMUTATONA(n,r)
Where:
n = the total number of items (in this case, metals)
r = the number of items being selected or arranged
Substituting the values:
n = 4 (four different metals)
r = 2 (selecting two metals for each arrangement)
The result is 16 different permutations.
The Excel 365 dynamic formula in cell I3 creates a list of permutations with repetition, I demonstrate a formula that creates permutations without repetition below.
Formula in cell I3:
This formula is dynamic meaning it spills to more or fewer cells automatically if you change the numbers in cells F5 and F6.
Explaining formula
Step 1 - Calculate items in list
The PERMUTATIONA function returns the number of permutations for a specific number of elements that can be selected from a larger group of elements. Repetition is allowed.
PERMUTATIONA(number, number-chosen)
PERMUTATIONA(F5, F6)
becomes
PERMUTATIONA(4, 2)
and returns 16.
Step 2 - Create a list of sequential numbers
The SEQUENCE function creates a list of sequential numbers to a cell range or array.
SEQUENCE(rows, [columns], [start], [step])
SEQUENCE(PERMUTATIONA(F5,F6))-1
becomes
SEQUENCE(16)-1
becomes
{1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}-1
and returns
{0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15}
Step 3 - Number raised to a power
^ character lets you raise a number to a power of a given number. It is the same as the POWER function but shorter.
F5^(SEQUENCE(,F6,F6-1,-1)+1)
becomes
F5^(SEQUENCE(,2,1,-1)+1)
becomes
F5^({1, 0}+1)
becomes
4^{2, 1}
and returns {16, 4}.
Step 4 - Calculate remainder
The MOD function returns the remainder after a number is divided by a divisor.
MOD(number, divisor)
MOD(SEQUENCE(PERMUTATIONA(F5,F6))-1,F5^(SEQUENCE(,F6,F6-1,-1)+1))
becomes
MOD({0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15},{16, 4})
and returns
{0, 0; 1, 1; 2, 2; 3, 3; 4, 0; 5, 1; 6, 2; 7, 3; 8, 0; 9, 1; 10, 2; 11, 3; 12, 0; 13, 1; 14, 2; 15, 3}.
Step 5 - Round numbers down
Thr FLOOR function rounds a number down, toward zero, to the nearest multiple of significance.
FLOOR(number, significance)
FLOOR(MOD(SEQUENCE(PERMUTATIONA(F5,F6))-1,F5^(SEQUENCE(,F6,F6-1,-1)+1))/(F5^SEQUENCE(,F6,F6-1,-1)),1)+1
becomes
FLOOR({0, 0; 1, 1; 2, 2; 3, 3; 4, 0; 5, 1; 6, 2; 7, 3; 8, 0; 9, 1; 10, 2; 11, 3; 12, 0; 13, 1; 14, 2; 15, 3}/({4,1}),1)+1
becomes
FLOOR({0, 0; 0.25, 1; 0.5, 2; 0.75, 3; 1, 0; 1.25, 1; 1.5, 2; 1.75, 3; 2, 0; 2.25, 1; 2.5, 2; 2.75, 3; 3, 0; 3.25, 1; 3.5, 2; 3.75, 3},1)+1
becomes
{0, 0; 0, 1; 0, 2; 0, 3; 1, 0; 1, 1; 1, 2; 1, 3; 2, 0; 2, 1; 2, 2; 2, 3; 3, 0; 3, 1; 3, 2; 3, 3}+1
and returns
{1, 1; 1, 2; 1, 3; 1, 4; 2, 1; 2, 2; 2, 3; 2, 4; 3, 1; 3, 2; 3, 3; 3, 4; 4, 1; 4, 2; 4, 3; 4, 4}.
Step 6 - Get values
The INDEX function gets a value based on a row number and column number (optional).
INDEX(array, [row_num], [column_num], [area_num])
INDEX(B3:E3,FLOOR(MOD(SEQUENCE(PERMUTATIONA(F5,F6))-1,F5^(SEQUENCE(,F6,F6-1,-1)+1))/(F5^SEQUENCE(,F6,F6-1,-1)),1)+1)
becomes
INDEX(B3:E3, {1, 1; 1, 2; 1, 3; 1, 4; 2, 1; 2, 2; 2, 3; 2, 4; 3, 1; 3, 2; 3, 3; 3, 4; 4, 1; 4, 2; 4, 3; 4, 4})
becomes
INDEX({"A","B","C","D"}, {1, 1; 1, 2; 1, 3; 1, 4; 2, 1; 2, 2; 2, 3; 2, 4; 3, 1; 3, 2; 3, 3; 3, 4; 4, 1; 4, 2; 4, 3; 4, 4})
and returns
{"A", "A"; "A", "B"; "A", "C"; "A", "D"; "B", "A"; "B", "B"; "B", "C"; "B", "D"; "C", "A"; "C", "B"; "C", "C"; "C", "D"; "D", "A"; "D", "B"; "D", "C"; "D", "D"}.
Step 7 - Shorten formula
The LET function lets you name intermediate calculation results which can shorten formulas considerably and improve performance.
LET(name1, name_value1, calculation_or_name2, [name_value2, calculation_or_name3...])
INDEX(B3:E3, FLOOR(MOD(SEQUENCE(PERMUTATIONA(F5,F6))-1,F5^(SEQUENCE(,F6,F6-1,-1)+1))/(F5^SEQUENCE(,F6,F6-1,-1)),1)+1)
becomes
LET(y, F6, x, SEQUENCE(,y,y-1,-1), INDEX(B3:E3,FLOOR(MOD(SEQUENCE(PERMUTATIONA(F5,y))-1,F5^(x+1))/(F5^x),1)+1))
Recommended articles
List permutations with repetition [UDF]
Create permutations [UDF]
Permutations with and without repetition
List all permutations with a condition
6. Function not working
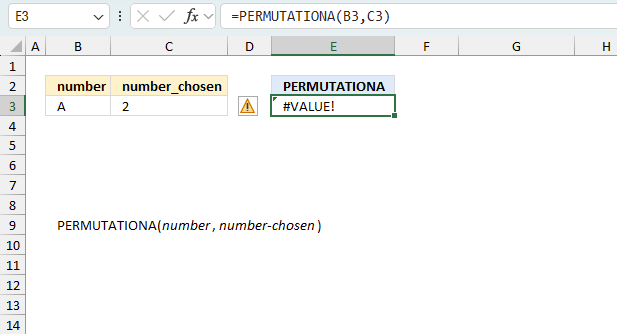
The PERMUTATIONA function returns:
- #NUM! error value if numeric arguments are values that are not valid.
- #VALUE! error value if numeric arguments use data types that are non-numeric.
6.1 Troubleshooting the error value
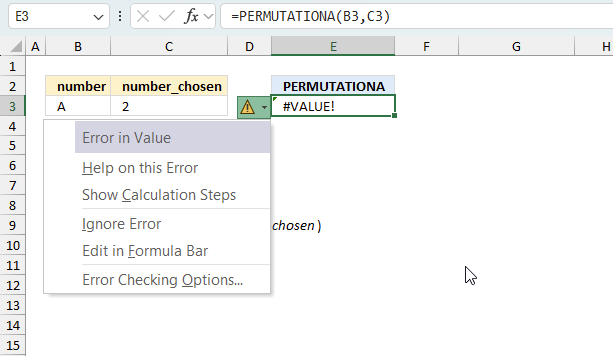
When you encounter an error value in a cell a warning symbol appears, displayed in the image above. Press with mouse on it to see a pop-up menu that lets you get more information about the error.
- The first line describes the error if you press with left mouse button on it.
- The second line opens a pane that explains the error in greater detail.
- The third line takes you to the "Evaluate Formula" tool, a dialog box appears allowing you to examine the formula in greater detail.
- This line lets you ignore the error value meaning the warning icon disappears, however, the error is still in the cell.
- The fifth line lets you edit the formula in the Formula bar.
- The sixth line opens the Excel settings so you can adjust the Error Checking Options.
Here are a few of the most common Excel errors you may encounter.
#NULL error - This error occurs most often if you by mistake use a space character in a formula where it shouldn't be. Excel interprets a space character as an intersection operator. If the ranges don't intersect an #NULL error is returned. The #NULL! error occurs when a formula attempts to calculate the intersection of two ranges that do not actually intersect. This can happen when the wrong range operator is used in the formula, or when the intersection operator (represented by a space character) is used between two ranges that do not overlap. To fix this error double check that the ranges referenced in the formula that use the intersection operator actually have cells in common.
#SPILL error - The #SPILL! error occurs only in version Excel 365 and is caused by a dynamic array being to large, meaning there are cells below and/or to the right that are not empty. This prevents the dynamic array formula expanding into new empty cells.
#DIV/0 error - This error happens if you try to divide a number by 0 (zero) or a value that equates to zero which is not possible mathematically.
#VALUE error - The #VALUE error occurs when a formula has a value that is of the wrong data type. Such as text where a number is expected or when dates are evaluated as text.
#REF error - The #REF error happens when a cell reference is invalid. This can happen if a cell is deleted that is referenced by a formula.
#NAME error - The #NAME error happens if you misspelled a function or a named range.
#NUM error - The #NUM error shows up when you try to use invalid numeric values in formulas, like square root of a negative number.
#N/A error - The #N/A error happens when a value is not available for a formula or found in a given cell range, for example in the VLOOKUP or MATCH functions.
#GETTING_DATA error - The #GETTING_DATA error shows while external sources are loading, this can indicate a delay in fetching the data or that the external source is unavailable right now.
6.2 The formula returns an unexpected value
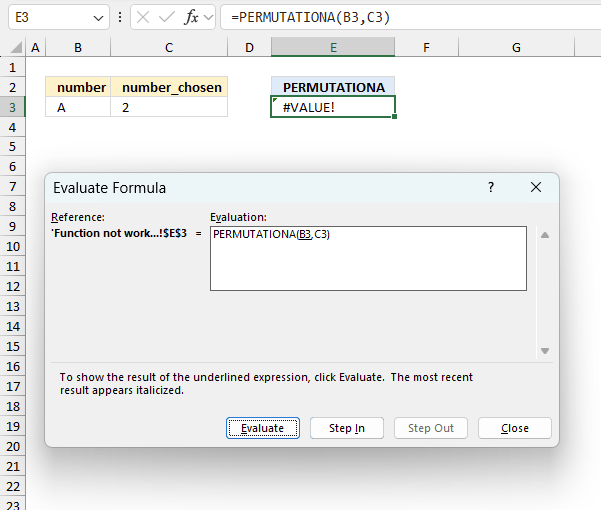
To understand why a formula returns an unexpected value we need to examine the calculations steps in detail. Luckily, Excel has a tool that is really handy in these situations. Here is how to troubleshoot a formula:
- Select the cell containing the formula you want to examine in detail.
- Go to tab “Formulas” on the ribbon.
- Press with left mouse button on "Evaluate Formula" button. A dialog box appears.
The formula appears in a white field inside the dialog box. Underlined expressions are calculations being processed in the next step. The italicized expression is the most recent result. The buttons at the bottom of the dialog box allows you to evaluate the formula in smaller calculations which you control. - Press with left mouse button on the "Evaluate" button located at the bottom of the dialog box to process the underlined expression.
- Repeat pressing the "Evaluate" button until you have seen all calculations step by step. This allows you to examine the formula in greater detail and hopefully find the culprit.
- Press "Close" button to dismiss the dialog box.
There is also another way to debug formulas using the function key F9. F9 is especially useful if you have a feeling that a specific part of the formula is the issue, this makes it faster than the "Evaluate Formula" tool since you don't need to go through all calculations to find the issue.
- Enter Edit mode: Double-press with left mouse button on the cell or press F2 to enter Edit mode for the formula.
- Select part of the formula: Highlight the specific part of the formula you want to evaluate. You can select and evaluate any part of the formula that could work as a standalone formula.
- Press F9: This will calculate and display the result of just that selected portion.
- Evaluate step-by-step: You can select and evaluate different parts of the formula to see intermediate results.
- Check for errors: This allows you to pinpoint which part of a complex formula may be causing an error.
The image above shows cell reference B3 converted to hard-coded value using the F9 key. The SORT function requires numerical values which is not the case in this example. We have found what is wrong with the formula.
Tips!
- View actual values: Selecting a cell reference and pressing F9 will show the actual values in those cells.
- Exit safely: Press Esc to exit Edit mode without changing the formula. Don't press Enter, as that would replace the formula part with the calculated value.
- Full recalculation: Pressing F9 outside of Edit mode will recalculate all formulas in the workbook.
Remember to be careful not to accidentally overwrite parts of your formula when using F9. Always exit with Esc rather than Enter to preserve the original formula. However, if you make a mistake overwriting the formula it is not the end of the world. You can “undo” the action by pressing keyboard shortcut keys CTRL + z or pressing the “Undo” button
6.3 Other errors
Floating-point arithmetic may give inaccurate results in Excel - Article
Floating-point errors are usually very small, often beyond the 15th decimal place, and in most cases don't affect calculations significantly.
7. List permutations with repetition and how many to choose from
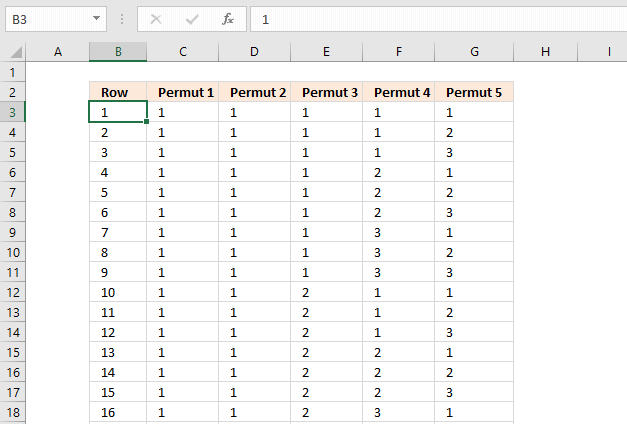
This section demonstrates a macro that lets you create a list of permutations, repetitions are allowed, based on a number of comma-delimited strings and the number of items per row.
The image above shows a list created by the macro based on numbers 1, 2, and 3 and five items per row.
Table of Contents
- Question
- VBA code
- Where to copy code?
- How to run the macro?
- How to use the macro?
- List permutations with repetition and how many to choose from (Excel 365 formula)
- Get the Excel File here
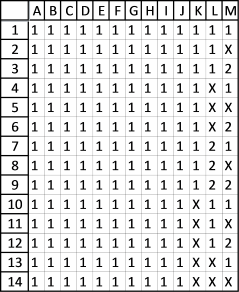
Noel asks:
Is there a way where I can predict all possible outcomes in Excel in the below example?
Total games are 13 (ABCDEFGHIJKLM). Possible outcomes are win(home team), draw or win(Away team) represented by 1, X or 2 respectively. Outcomes should be in the below formats:
111111111111X
11111111111XX
2222222X22221
222222222222X
7.2. VBA code
The following macro lets you enter text strings separated by a comma and the number of games.
Sub ListPermut()
'This macro creates a list of all permutations
'Get digital Help - https://www.get-digital-help.com/
'Define variables
Dim ws As Worksheet, Ans As String, ans1() As String, digits As Integer
Dim num As Integer, p As Long, i As Long, t As Long
Dim rng() As Long, c As Long, rng1() As String
'Insert a new sheet
Set ws = Sheets.Add
'Ask for user input
Ans = InputBox("Type strings separated with a comma:")
digits = InputBox("How many strings?")
'Split text strings to an array
ans1 = Split(Ans, ",")
'Count values in aray
num = UBound(ans1) + 1
'Calculate number of permutations
p = num ^ digits
'Redimension arrays
ReDim rng(1 To digits)
ReDim rng1(1 To digits)
'Save 1 to all values in first row of array
For c = 1 To digits
rng(c) = 1
Next c
i = 0
'Don't show the result until finished
Application.ScreenUpdating = False
'Repeat until all permutations have been created
Do Until (i + t) = (p - 1)
'Use text strings instead of numbers
For c = LBound(rng1) To UBound(rng1)
rng1(c) = ans1(rng(c) - 1)
Next c
'Transfer values from array to worksheet
ws.Range("A1").Resize(, digits).Offset(i) = rng1
'Build next row of permutations
For c = digits To 1 Step -1
If c = digits Then
rng(c) = rng(c) + 1
ElseIf rng(c) = 0 Then
rng(c) = rng(c - 1)
End If
If rng(c) = num + 1 Then
rng(c) = 1
rng(c - 1) = rng(c - 1) + 1
End If
Next c
'Count made permutations
i = i + 1
'Insert a new sheet if rows exceed 999 999
If i = 1000000 Then
Set ws = Sheets.Add
t = t + 1000000
i = 0
End If
Loop
'Use text strings instead of numbers
For c = LBound(rng1) To UBound(rng1)
rng1(c) = ans1(rng(c) - 1)
Next c
'Transfer values from array to worksheet
ws.Range("A1").Resize(, digits).Offset(i) = rng1
'Show output
Application.ScreenUpdating = True
End Sub
7.3. Where to copy code?
- Press Alt-F11 to open visual basic editor
- Press with left mouse button on Module on the Insert menu
- Copy and paste code above to the code module
- Exit visual basic editor (Alt+Q)
7.4. How to run the macro?
- Press Alt+F8 to open the macro dialog box
- Press with left mouse button on ListPermut macro
- Press with left mouse button on Run.
7.5. How to use the macro?
Enter your text strings using a comma as a text delimiting character.
Press with left mouse button on OK button.
Enter number of games.
Press with left mouse button on OK button.
Excel processes the data for a while and then creates two sheets with a total of 1594323 permutations.
The picture shows 14 out of 1594323 permutations.
7.6. List permutations with repetition and how many to choose from (Excel 365 formula)
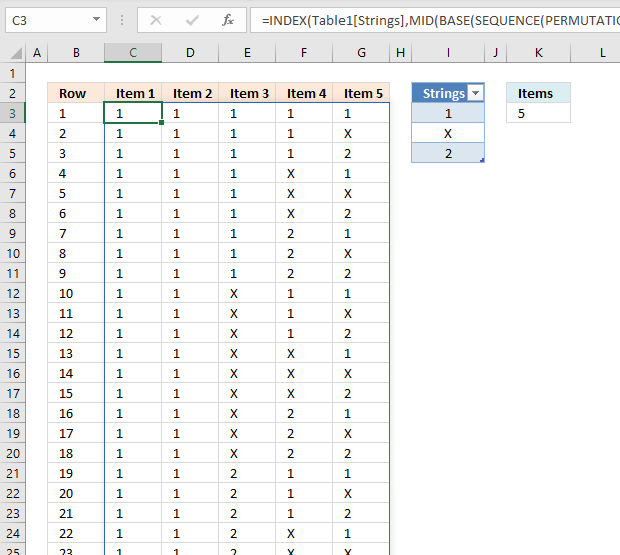
The Excel 365 formula in cell C3 spills to other adjacent cells automatically based on the values in the Excel Table (cell range I3:I5) and the number entered in cell K3.
You can add and delete strings in cell range I3:I5, the only limit is the worksheet row limit of 1 048 576. For example, 3 strings and 13 items return 1 594 323 rows and won't fit a worksheet.
You have to move the Excel Table and the value in cell K3 if you have more than 6 items, the Excel 365 formula returns a #SPILL! error if adjacent cells are populated.
Excel 365 dynamic array formula in cell C3:
Excel 365 formula in cell B3:
8. List all permutations with a condition
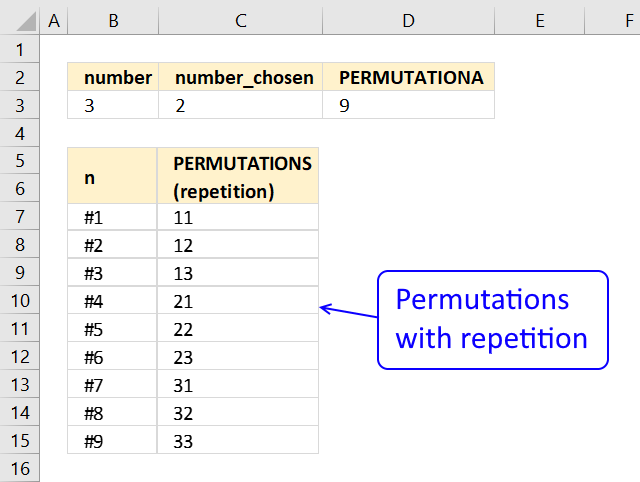
I got a question a while ago about permutations, in essence how to find every permutation between 0 and 9 000 000 000 with a condition, if the sum of all digits in a number is smaller or equal to 9.
You can read about the difference between combinations and permutations here: Return all combinations but in short, the order is important for permutations and not important for combinations.
This number 303 030 000 is equal to 9 if you sum every digit, 3+0+3+0+3+0+0+0+0 = 9. 92 is above 9, 9+2 = 11 and is not a number we are looking for.
What's on this section
- Sum all digits in a number - User Defined Function (UDF)
- Sum all digits in a number - (formula)
- Generate permutations based on a condition (slow UDF)
- Generate permutations based on a condition (faster UDF)
- Comparing custom functions
- Where to put the code?
- Get the Excel File here
8.1. Sum all digits in a number - User Defined Function (UDF)
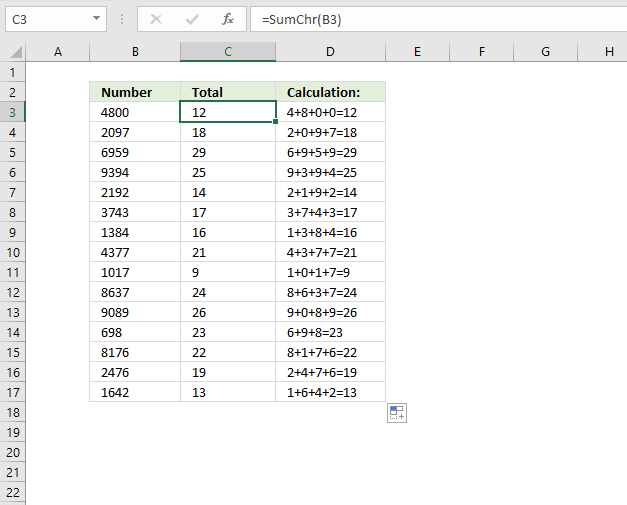
The following user-defined function named SumChr adds all digits in a number and returns the total. The image above demonstrates the SumChr function in column B.
For example, number 92 in cell A3 contains two digits, 9 and 2. The total is 9 + 2 equals 11. The SumChr function returns 11 in cell B3.
'Name User Defined Function and specify parameters Function SumChr(nmbr As Long) 'Dimension variables and declare data types Dim sm As Long 'For ... Next statement For i = 1 To Len(CStr(nmbr)) 'Add number to total and save the total sm = sm + Val(Mid(nmbr, i, 1)) 'Continue with next digit Next i 'Return total to worksheet SumChr = sm End Function
8.2. Sum all digits in a number (formula)
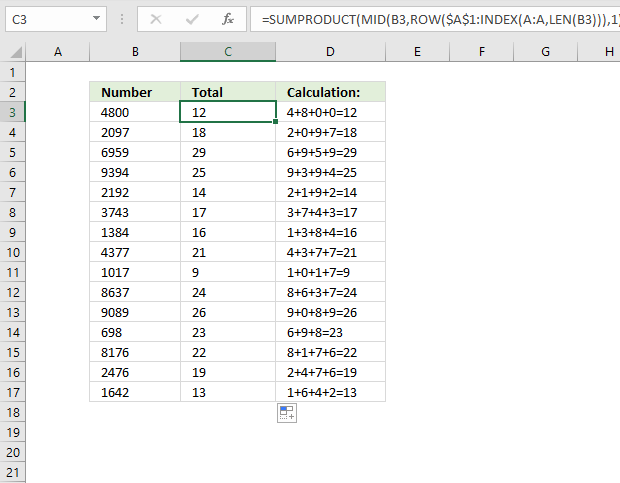
Formula in cell C3:
Excel 365 dynamic array formula in cell C3:
8.3. Generate permutations based on a condition (slow UDF)
It is easy to iterate through every number between 0 and for example 10 000 000 and check if the digit sum is smaller or equal to 9. The UDF below does that.
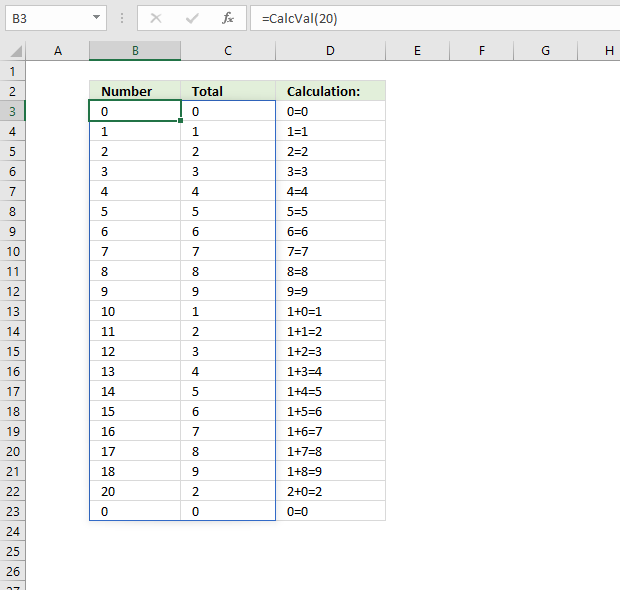
The picture above shows all numbers between 0 and 20 where the digit sum is smaller or equal to 9, the CalcVal function above made this list.
Number 19 is missing, 1+9 = 10. 10 is bigger than 9. Column B contains the digit sum, except cell B1. It has the time it took to calculate the list. In this case, it took almost no time at all, and excel rounded it to 0 (zero).
'Name User Defined Function and specify parameters Function CalcVal(k As Double) 'Dimension variables and declare data types Dim i As Long, j() As Double, a As Double 'Redimension array variable j ReDim j(0 To 60000, 1) 'Save timer value to variable a a = Timer 'Save 0 (zero) to variable l l = 0 'For ... Next statement 'Iterate from 0 (zero) to number stored in variable k For i = 0 To k 'Calculate total using UDF SumChr based on number stored in variable i m = SumChr(i) Check if variable m is equal to 9 If m <= 9 Then 'Save value stored in variable i to array variable j j(l, 0) = i 'Save value stored in variable m to array variable j j(l, 1) = m 'Add one to value stored in variable l and save to variable l l = l + 1 End If Next i 'Calculate time needed calculate result and save to array variable j j(0, 1) = Timer - a 'Return array variable j to worksheet CalcVal = j() End Function
8.4. Generate permutations based on a condition (faster UDF)
The problem is if you try to do the same with a really large range of numbers, it will take a very long time to calculate for a desktop pc. This UDF shortens that time considerably.
'Name User Defined Function and specify parameters Function CalcVal1(k As Single) 'Dimension variables and declare data types Dim i As Single, j() As Double, a As Double Dim l As Single, m As Single 'Save time value to variable a a = Timer 'Redimension array variable j ReDim j(0 To 2000000, 1) 'Save -1 to variable i and 0 (zero) to variable m i = -1: m = 0 'Do Until ... Loop 'Keep iterating until number in variable k is maller than or equal to number in variable i Do Until k <= i 'If ... Then .. ElseIf .. Endif statement 'Check if total is equal to or less than 9 If SumChr(i) <= 9 Then 'Convert variable i to string and then count characters in string, save number of characters to variable p p = Len(CStr(i)) 'For ... Next statement 'Go backwards from number of characters in variable i to 1 For l = Len(CStr(i)) To 1 Step -1 'If ... Then ... ElseIf ... Esle ... End If statement 'Check if characters is not equal to 0 (zero) and not equal to 9 If Mid(i, l, 1) <> 0 And Mid(i, l, 1) <> 9 Then 'Replace character in string i = Val(ReplaceChrInStr(i, l, 0)) i = Val(ReplaceChrInStr(i, l - 1, Mid(i, l - 1, 1) + 1)) Exit For ElseIf Mid(i, l, 1) = 9 Then i = i + Application.WorksheetFunction.Power(10, Len(CStr(i)) - 1) Exit For End If Next l Else i = i + 1 End If If i < k Then j(m, 0) = i Else j(m, 0) = "" End If j(m, 1) = SumChr(i) m = m + 1 Loop j(0, 1) = Timer - a CalcVal1 = j End Function
Function ReplaceChrInStr(tmp As String, pos As Single, chr As String)
Dim str As String, i As Single
For i = 1 To Len(tmp)
If i = pos Then
str = str & chr
Else
str = str & Mid(tmp, i, 1)
End If
Next i
ReplaceChrInStr = str
End Function
The UDF basically examines each digit in a number and if the sum is 9 these things happens:
- If digit is not equal to 9 and zero, make that digit a 0 and add 1 to the next digit.
- If digit is equal to 9, add 1,10, 100... depending on the position (n) the digit has in the number. Example, digit 9 in number 90 is the second digit counting from right to left, n=2. 10^(2-1) is 10. 90+10 = 100
If the digit sum is not equal to 9 the udf adds 1 to the current number and the loop continues until the entire range has been created.
8.5. Comparing custom functions
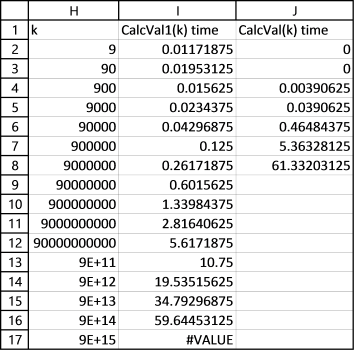
Now lets compare the run times of the two udfs CalcVal and CalcVal1.
For smaller ranges like 0 - 9000 CalcVal is faster, somewhere around perhaps 5000 CalcVal1 seems to take the lead.
I am using an old laptop with a dual-core intel i3 cpu, I am getting 29% utilization. I don't know why, it seems that only one core is utilized by excel. In any case, the numbers indicate that the CalcVal1 function is much faster.
8.6. Where to put the code?
- Press Alt + F11 to open the Visual Basic Editor (VBE).
- Press with mouse on "Insert" on the top menu.
- Press with mouse on "Module".
- Copy above UDFs and paste to the code window.
- Return to Excel
'PERMUTATIONA' function examples
Functions in 'Statistical' category
The PERMUTATIONA function function is one of 73 functions in the 'Statistical' category.
Excel function categories
Excel categories
4 Responses to “How to use the PERMUTATIONA function”
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.

I have 17 games to bet, and am suppose to choose win, loose and draw.
How can I create a table with 17,matches with win,lose and draw? How many table will appear?
jimmy munisi,
The outcome is either win, lose or draw, three possibilities.
There are 17 games. 3^17 = 129 140 163 permutations.
If you want to list all permutations in a workbook, each sheet has 1 048 576 rows.
129 140 163 / 1 048 576 = 123.1 sheets
You need 124 worksheets in a workbook to list all permutations.
Hi, if I create a table with more than 10 elements, I get an error in all the cells that should contain an element >10. I would like to know how I could resolve. Thanks!
=INDEX(Table1[Strings], MID(BASE(SEQUENCE(PERMUTATIONA(COUNTA(Table1[Strings]),$K$3))-1, COUNTA(Table1[Strings]), $K$3), SEQUENCE(, $K$3), 1)+1) Using this formula. Sorry I forgot to specify.