How to use the STDEVA function

The STDEVA function estimates the standard deviation from a sample of values. It evaluates Boolean value TRUE as 1, FALSE and text values as 0 (zero).

1. Introduction

What is Standard Deviation?

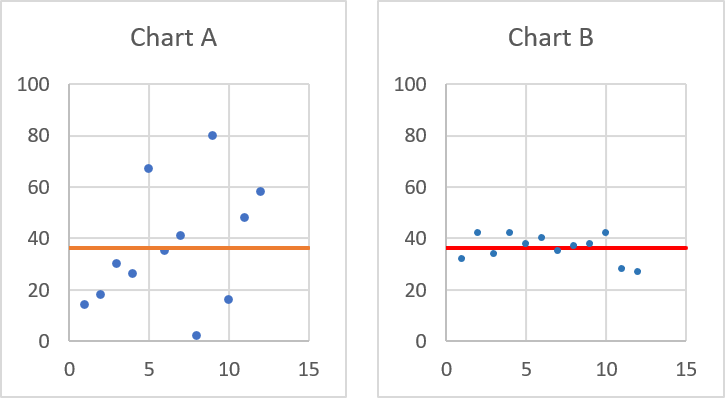
Standard deviation tells you how far from the average values are spread out. Both charts above have numbers and an average plotted, they share the exact same average however, the numbers are not the same.

Chart A above shows that the values are more spread out than the values in chart B. Chart A has a standard deviation of 23.45256334, standard deviation for chart B is 5.207075606. Standard deviation is fundamental in statistics.

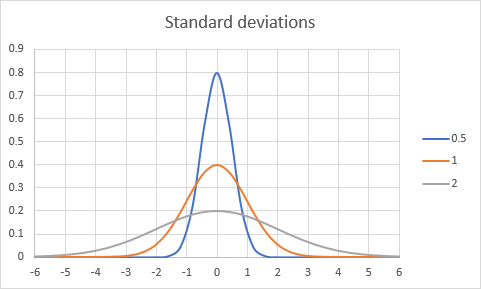
A normal distribution is a symmetric, bell-shaped probability distribution that is commonly used in statistics and probability theory. The shape of the normal distribution is determined by its mean (μ) and standard deviation (σ). The mean represents the center of the distribution, while the standard deviation represents the spread or dispersion of the data around the mean.

• A normal distribution with a standard deviation of 0.5 is relatively narrow and tightly clustered around the mean.
  
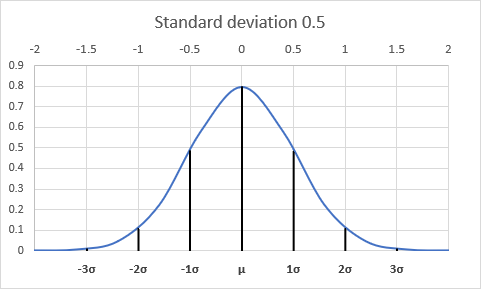
  The values in the distribution are concentrated within a smaller range, with most values falling closer to the mean. The curve appears tall and steep, indicating a higher concentration of data points near the mean.
• A normal distribution with a standard deviation of 1 is the most commonly used normal distribution, often referred to as the standard normal distribution.
  
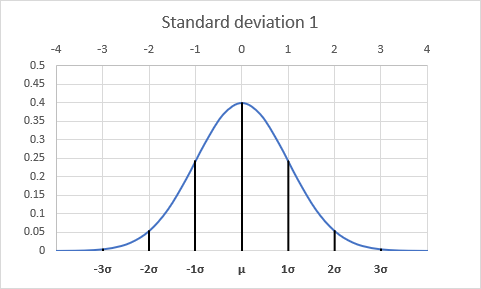
  The standard deviation of 1 represents a moderate spread of the data around the mean. About 68% of the data falls within one standard deviation (±1σ) of the mean, and approximately 95% of the data falls within two standard deviations (±2σ) of the mean. The curve has a characteristic bell shape, with a smooth and gradual taper towards the tails.
• A normal distribution with a standard deviation of 2 is relatively wide and spread out compared to the standard normal distribution. The data is dispersed over a larger range, with values more spread out from the mean. The curve appears shorter and flatter, indicating a lower concentration of data points near the mean.

When to use the STDEV.P function and the STDEV.S function?

Use STDEV.P if you have the full population data. Use STDEV.S if you have a sample of limited data from a larger population. STDEV.P will result in a lower standard deviation compared to STDEV.S on the same data.

Sample standard deviation is considered a better estimate for inferring population parameters.

What is inferring population parameters?

Population parameters refer to the actual values of statistics that describe an entire population, such as the population mean or standard deviation. However, the true population parameter values are often not known.

What is sample inferential statistics?

Sample inferential statistics are methods that allow using statistics calculated on a sample of data to infer the unknown population parameters.

For example:

• The sample mean can be used to estimate the population mean.
• The sample standard deviation can estimate the population standard deviation.

What is the difference between the STDEVA function and the STDEV.S function?

The STDEVA function evaluates:

• Boolean value TRUE as 1
• FALSE is 0 (zero).
• Text values are evaluated as 0 (zero) as well.

The STDEV.S function ignores Boolean and text values. estimates the standard deviation from a sample of values. Both formulas use the same math formula to calculate the standard deviation.

What is the difference between the STDEVA function and the STDEVPA function?

The STDEVA function estimates the standard deviation from a sample of values. If your data contains the entire population use instead the STDEVPA function to calculate the standard deviation.

Both functions evaluate:

• Boolean value TRUE as 1.
• FALSE is 0 (zero).
• Text values are evaluated as 0 (zero) as well.

STDEVPA math formula:

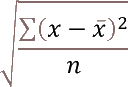
STDEVPA function = √(Σ(x - x̄)²/n)

STDEVA math formula:

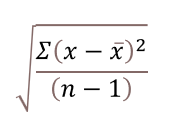
STDEVA function = √(Σ(x - x̄)²/(n-1))

How can standard deviation be used to find outliers?

Standard deviation can be used to identify potential outliers in a dataset by defining a range based on the mean and standard deviation values. Observations that fall outside this range are considered outliers.

A common approach is to use the range μ ± 3σ, which covers approximately 99.7% of the data points if the distribution is normal.

Values below (μ - 3σ) are considered potential lower outliers.
Values above (μ + 3σ) are considered potential upper outliers.

μ - the mean
σ - standard deviation

What is the 68–95–99.7 rule?

The 68–95–99.7 rule, also known as the Empirical Rule, is a useful statistical principle that describes the percentage of data values that fall within certain standard deviations from the mean in a normal distribution.

• 68% of the data falls between μ ± 1σ
• 95% of the data falls between μ ± 2σ
• 99.7% of the data falls between μ ± 3σ

It's important to note that the 68–95–99.7 rule is an approximation and assumes that the data follows a normal distribution. In cases of skewed or heavy-tailed distributions the percentages may not hold true.  Alternative methods may be needed to describe the data spread accurately.

2. STDEVA Function Syntax

STDEVA(number1,[number2],...)

3. Arguments

number1	Required. This argument can be an array of constants or a cell reference to a group of values.
[number2]	Optional. Up to 254 additional arguments.

4. Example

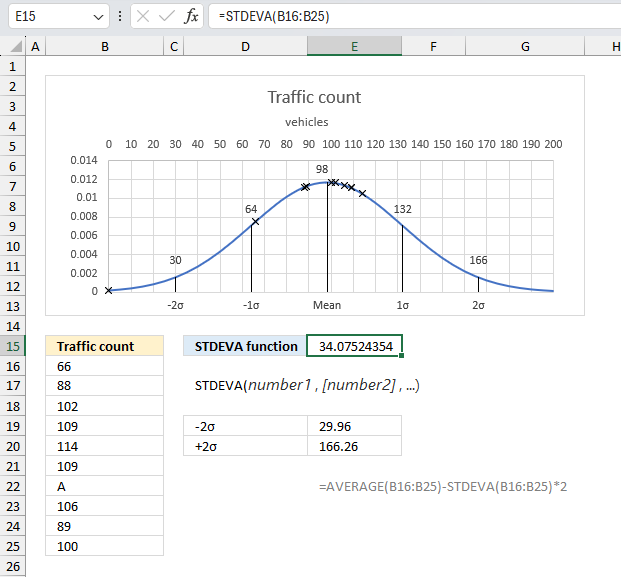
A transportation analyst has collected data on the number of vehicles passing through a certain road section during specified time intervals. Assume the data follows a normal distribution. Find the outliers outside the 2 standard deviations (±2σ) range?

The data is:

Traffic
66
88
102
109
114
109
A
106
89
100

The argument is:

number1 = B16:B25

The data points are specified in cells B16:B25 in the image above.

The image above shows a chart containing a blue curve representing the probability mass function of a normal distribution where the mean is 98 and the standard deviation is 34.08, calculated below. The chart shows the standard deviations denoted ±1σ, ±2σ, and ±3σ, cells E19:E20 display ±2σ standard deviation. 2σ = 29.96 and -2σ = 166.26

Formula in cell E15:

Cell E15 displays 34.08 which represents the standard deviation (σ) based on the values in B15:B25. We can use this value and the arithmetic mean to calculate the ±2σ standard deviations.

Formula in cell E19:

The formula in cell E19 first calculates the arithmetic mean using the AVERAGE function. It then takes this mean value and subtracts twice the standard deviation from it. Specifically, it subtracts the product of 34.08 and 2 from 99, resulting in a value of 70.25.

98.11 - (34.08 × 2) = 98.1111111111111 - 68.1504870774149 = 29.96

Formula in cell E20:

The formula in cell E20 uses the AVERAGE function to calculate the arithmetic mean then calculates the total with the standard deviation multiplied by 2.

98.11 + (34.08 × 2) = 98.1111111111111 + 68.1504870774149 = 166.26

The chart in the image above shows a normal distribution with the standard deviations denoted ±1σ, ±2σ, and ±3σ. One data point is outside the ±2σ standard deviations which is 0 (zero) representing the text string "A" in cell B22.

5. How is the function calculated?

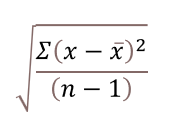
STDEVA function = √(Σ(x - x̄)²/(n-1))

x̄ - arithmetic mean
n - count of values

To calculate the standard deviation based on a sample using only three numbers follow these steps:

1. Find the mean (average) of the three numbers.
   - Let's say the three numbers are x₁, x₂, and x₃.
   - The mean (x̄) is calculated as: x̄ = (x₁ + x₂ + x₃) / 3
2. Calculate the deviation of each number from the mean.
   - Deviation of x1 from the mean: x₁ - x̄
   - Deviation of x2 from the mean: x₂ - x̄
   - Deviation of x3 from the mean: x₃ - x̄
3. Square each of the deviations.
   (x₁ - x̄)²
   (x₂ - x̄)²
   (x₃ - x̄)²
4. Find the sum of the squared deviations.
   - Sum of squared deviations = (x₁ - x̄)² + (x₂ - x̄)² + (x₃ - x̄)²
5. Divide the sum of squared deviations by (n - 1), where n is the number of data points (in this case, n = 3).
   - Variance = Sum of squared deviations / (n - 1)
   - Variance = Sum of squared deviations / 2
6. Take the square root of the variance to obtain the standard deviation.
   - Standard deviation = √(Variance)

6. Function not working

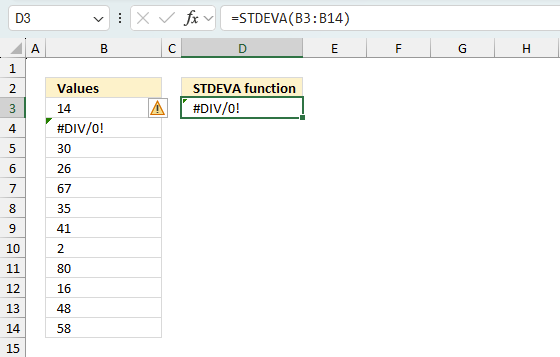
The STDEVA function returns

• #NAME? error if you misspell the function name.
• propagates errors, meaning that if the input contains an error (e.g., #VALUE!, #REF!), the function will return the same error.

6.1 Troubleshooting the error value

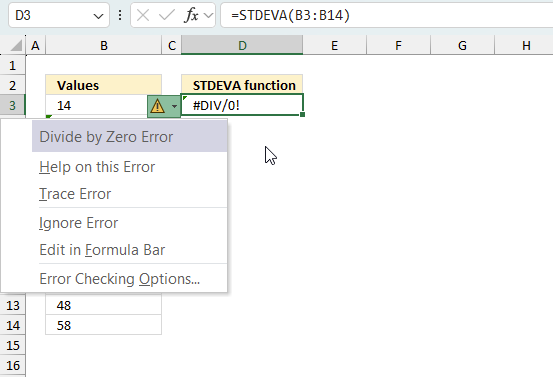
When you encounter an error value in a cell a warning symbol appears, displayed in the image above. Press with mouse on it to see a pop-up menu that lets you get more information about the error.

1. The first line describes the error if you press with left mouse button on it.
2. The second line opens a pane that explains the error in greater detail.
3. The third line takes you to the "Evaluate Formula" tool, a dialog box appears allowing you to examine the formula in greater detail.
4. This line lets you ignore the error value meaning the warning icon disappears, however, the error is still in the cell.
5. The fifth line lets you edit the formula in the Formula bar.
6. The sixth line opens the Excel settings so you can adjust the Error Checking Options.

Here are a few of the most common Excel errors you may encounter.

#NULL error - This error occurs most often if you by mistake use a space character in a formula where it shouldn't be. Excel interprets a space character as an intersection operator. If the ranges don't intersect an #NULL error is returned. The #NULL! error occurs when a formula attempts to calculate the intersection of two ranges that do not actually intersect. This can happen when the wrong range operator is used in the formula, or when the intersection operator (represented by a space character) is used between two ranges that do not overlap. To fix this error double check that the ranges referenced in the formula that use the intersection operator actually have cells in common.

#SPILL error - The #SPILL! error occurs only in version Excel 365 and is caused by a dynamic array being to large, meaning there are cells below and/or to the right that are not empty. This prevents the dynamic array formula expanding into new empty cells.

#DIV/0 error - This error happens if you try to divide a number by 0 (zero) or a value that equates to zero which is not possible mathematically.

#VALUE error - The #VALUE error occurs when a formula has a value that is of the wrong data type. Such as text where a number is expected or when dates are evaluated as text.

#REF error - The #REF error happens when a cell reference is invalid. This can happen if a cell is deleted that is referenced by a formula.

#NAME error - The #NAME error happens if you misspelled a function or a named range.

#NUM error - The #NUM error shows up when you try to use invalid numeric values in formulas, like square root of a negative number.

#N/A error - The #N/A error happens when a value is not available for a formula or found in a given cell range, for example in the VLOOKUP or MATCH functions.

#GETTING_DATA error - The #GETTING_DATA error shows while external sources are loading, this can indicate a delay in fetching the data or that the external source is unavailable right now.

6.2 The formula returns an unexpected value

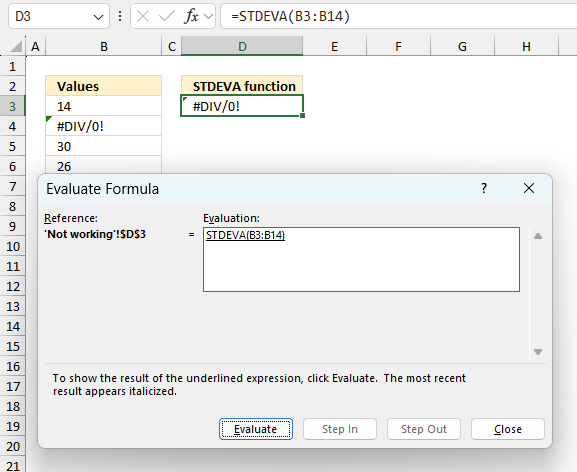
To understand why a formula returns an unexpected value we need to examine the calculations steps in detail. Luckily, Excel has a tool that is really handy in these situations. Here is how to troubleshoot a formula:

1. Select the cell containing the formula you want to examine in detail.
2. Go to tab “Formulas” on the ribbon.
3. Press with left mouse button on "Evaluate Formula" button. A dialog box appears.
   The formula appears in a white field inside the dialog box. Underlined expressions are calculations being processed in the next step. The italicized expression is the most recent result. The buttons at the bottom of the dialog box allows you to evaluate the formula in smaller calculations which you control.
4. Press with left mouse button on the "Evaluate" button located at the bottom of the dialog box to process the underlined expression.
5. Repeat pressing the "Evaluate" button until you have seen all calculations step by step. This allows you to examine the formula in greater detail and hopefully find the culprit.
6. Press "Close" button to dismiss the dialog box.

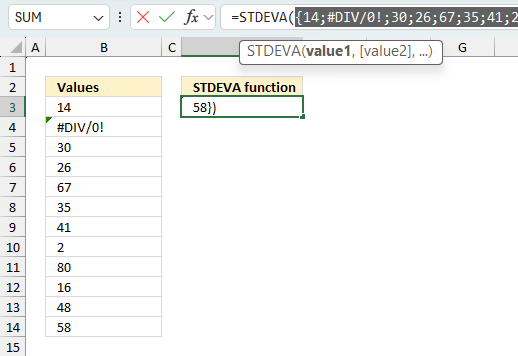
There is also another way to debug formulas using the function key F9. F9 is especially useful if you have a feeling that a specific part of the formula is the issue, this makes it faster than the "Evaluate Formula" tool since you don't need to go through all calculations to find the issue..

1. Enter Edit mode: Double-press with left mouse button on the cell or press F2 to enter Edit mode for the formula.
2. Select part of the formula: Highlight the specific part of the formula you want to evaluate. You can select and evaluate any part of the formula that could work as a standalone formula.
3. Press F9: This will calculate and display the result of just that selected portion.
4. Evaluate step-by-step: You can select and evaluate different parts of the formula to see intermediate results.
5. Check for errors: This allows you to pinpoint which part of a complex formula may be causing an error.

The image above shows cell reference B3:B14 converted to hard-coded value using the F9 key. The STDEVA function requires non-error values which is not the case in this example. We have found what is wrong with the formula.

Tips!

• View actual values: Selecting a cell reference and pressing F9 will show the actual values in those cells.
• Exit safely: Press Esc to exit Edit mode without changing the formula. Don't press Enter, as that would replace the formula part with the calculated value.
• Full recalculation: Pressing F9 outside of Edit mode will recalculate all formulas in the workbook.

Remember to be careful not to accidentally overwrite parts of your formula when using F9. Always exit with Esc rather than Enter to preserve the original formula. However, if you make a mistake overwriting the formula it is not the end of the world. You can “undo” the action by pressing keyboard shortcut keys CTRL + z or pressing the “Undo” button

6.3 Other errors

Floating-point arithmetic may give inaccurate results in Excel - Article

Floating-point errors are usually very small, often beyond the 15th decimal place, and in most cases don't affect calculations significantly.

Functions in 'Statistical' category

The STDEVA function function is one of 73 functions in the 'Statistical' category.

Excel function categories

Excel categories

Leave a Comment