How to create permutations
I discussed the difference between permutations and combinations in my last post, today I want to talk about two kinds of permutations, with repetition and without repetition.
What's on this webpage
1. Permutations with repetition
I explained in my last post that phone numbers are permutations because the order is important. But phone numbers may also contain duplicate numbers or repeated numbers like 11 234, here number 1 is repeated. A digit in a phone number has 10 different values, 0 to 9. A five digit phone number has 10x10x10x10x10 or 10^5 equals 100 000 permutations.
Another example with repetitive numbers are bits and bytes. A bit is a single binary number like 0 or 1. A byte is a sequence of bits and eight bits equal one byte. A byte contains 256 different permutations and repetition is allowed.
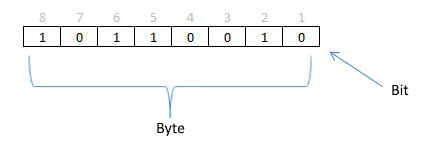
Here is how you calculate the number of permutations. There are two different values 0 and 1 (binary) and a byte has 8 binary values. 2x2x2x2x2x2x2x2 or 2^8 equals 256 permutations.
Did you know? The UTF-8 is a character encoding scheme using 8 bits to encode all possible characters, it is the most used encoding system on world wide web today.
2. Constructing a permutations array with binary values
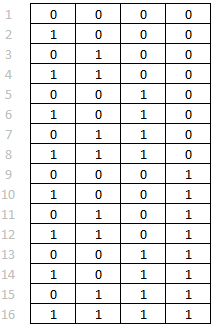 Excelxor showed us how to build a permutations array using only excel functions, in one of his blog posts.
Excelxor showed us how to build a permutations array using only excel functions, in one of his blog posts.
The picture to the left is an array made by excelxor's formula, this example uses four cells or 4 bits. 2x2x2x2 or 2^4 equals 16 permutations.
With this type of array excelxor finds which numbers add up to a total.
Array formula:
I have made a blog post a few years ago how to calculate permutations with repetition with a custom function.
Explaining array formula
Step 1 - Calculate number of rows
The ROWS function returns the number of rows in a cell range.
ROWS($A$2:$A$5)
returns 4.
Step 2 - Concatenate characters
The ampersand character concatenates strings and numbers.
"1:"&ROWS($A$2:$A$5) returns "1:4"
Step 3 - Create a cell reference
The INDIRECT function returns the reference specified by a text string.
INDIRECT("1:"&ROWS($A$2:$A$5)) returns cell reference 1:4
Step 4 - Return row numbers from cell reference
The ROW function returns the row number from a cell reference.
ROW( INDIRECT("1:"&ROWS($A$2:$A$5))) returns {1; 2; 3; 4}. These numbers are in a vertical range.
Step 5 - Transpose numbers
The TRANSPOSE function converts a vertical range to a horizontal range or vice versa.
TRANSPOSE( ROW( INDIRECT("1:"&ROWS($A$2:$A$5)))) returns {1, 2, 3, 4}.
Step 6 - Subtract with 1
( TRANSPOSE( ROW( INDIRECT("1:"&ROWS($A$2:$A$5))))-1 ) returns {0, 1, 2, 3}
Step 7 - Remove decimals from numbers
The INT function removes the decimal part from positive numbers and returns the whole number (integer) except negative values are rounded down to the nearest integer.
INT(( ROW( INDIRECT("1:"&2^ROWS($A$2:$A$5)))-1 )/2^( TRANSPOSE( ROW( INDIRECT("1:"&ROWS($A$2:$A$5))))-1 ))
returns {0, 0, 0, ... , 1}.
Step 8 - Create binary array
The MOD function returns the remainder after a number is divided by divisor.
MOD(INT(( ROW( INDIRECT("1:"&2^ROWS($A$2:$A$5)))-1 )/2^( TRANSPOSE( ROW( INDIRECT("1:"&ROWS($A$2:$A$5))))-1 )), 2)
returns {0, 0, 0, ... , 1}.
3. Permutations without repetition
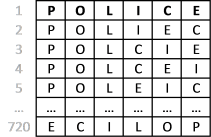 Imagine constructing an anagram of a word "police". You are allowed to rearrange the letters but you can´t repeat a letter. See picture to the right.
Imagine constructing an anagram of a word "police". You are allowed to rearrange the letters but you can´t repeat a letter. See picture to the right.
Another example is how many times can you rearrange 6 people around a table? Most people will get annoyed if you ask them to change seat more than once but in this example you can rearrange as many times as you like. How many permutations are there? You can´t have a person on two chairs at the same time, repetition is not allowed.
Here is a link to a udf I made a few years ago: Excel udf: List permutations without repetition
Tip! Use the PERMUT function to calculate permutations. The word police has 6 letters, how many permutations without repetition are there if you choose 6 out of 6 letters?
=PERMUT(6,6) equals 720 permutations.
4. Create permutations - UDF
Maximum Number Allowed is 4 digit and the number is from 0 to 9.
After I fill in the number i want it to automatic permutate the numbers and list in details, example if i key in 1234 and the list will be:
1234, 1243, 1423, 4123, 1324, 1342, 1432, 4132, 3124, 3142, 3412, 4312, 2134, 2143, 2413, 4213, 2314, 2341, 2431, 4231, 3214, 3241, 3421, 4321.
Answer:
This udf creates permutations from a text string. You can also choose how many letters in each permutation.
Array formula in cell A3:A26:
How to create this array formula
- Select cell range A3:A26
- Type above array formula in formula bar
- Press and hold Ctrl + Shift
- Press Enter once
- Release all keys
VBA code
Function ListPermut(str As String, num As Integer)
'Permutations without repetition
Dim c, r, p As Long
Dim rng() As Long, temp As Long, i As Long
Dim temp1 As Long, y() As Long, d As Long
Dim tmpOut(), tmpArr() As Variant
Dim j As Integer
Dim a As Boolean
ReDim tmpArr(0)
ReDim tmpOut(0)
For j = 1 To Len(str)
tmpArr(UBound(tmpArr)) = Mid(str, j, 1)
ReDim Preserve tmpArr(UBound(tmpArr) + 1)
Next j
ReDim Preserve tmpArr(UBound(tmpArr) - 1)
p = WorksheetFunction.Permut(Len(str), Len(str))
ReDim rng(1 To p, 1 To Len(str))
For c = 1 To Len(str)
rng(1, c) = c
Next c
For r = 2 To p
For c = 1 To num
tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut)) & tmpArr(rng(r - 1, c) - 1)
Next c
If UBound(tmpOut) <> 0 Then
If tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut) - 1) Then
tmpOut(UBound(tmpOut)) = ""
Else
ReDim Preserve tmpOut(UBound(tmpOut) + 1)
End If
Else
ReDim Preserve tmpOut(UBound(tmpOut) + 1)
End If
For c = Len(str) To 1 Step -1
If rng(r - 1, c - 1) < rng(r - 1, c) Then temp = c - 1 Exit For End If Next c For c = Len(str) To 1 Step -1 rng(r, c) = rng(r - 1, c) Next c For c = Len(str) To 1 Step -1 If rng(r - 1, c) > rng(r - 1, temp) Then
temp1 = rng(r - 1, temp)
rng(r, temp) = rng(r - 1, c)
rng(r, c) = temp1
ReDim y(Len(str) - temp)
i = 0
For d = temp + 1 To Len(str)
y(i) = rng(r, d)
i = i + 1
Next d
i = 0
For d = Len(str) To temp + 1 Step -1
rng(r, d) = y(i)
i = i + 1
Next d
Exit For
End If
Next c
If r = p Then
For c = 1 To num
tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut)) & tmpArr(rng(r, c) - 1)
Next c
If tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut) - 1) Then
ReDim Preserve tmpOut(UBound(tmpOut) - 1)
End If
End If
Next r
ListPermut = Application.Transpose(tmpOut)
End Function
Where to copy vba code?
Press Alt+F11
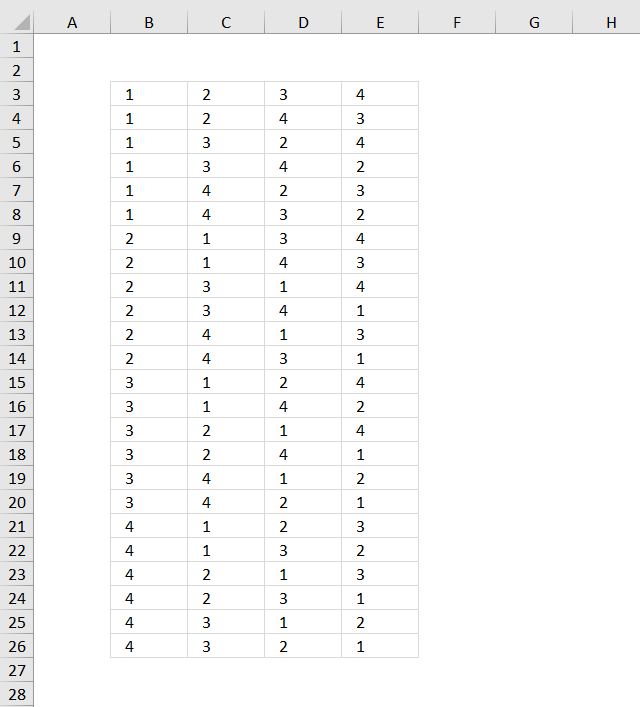
5. List permutations no repetition - UDF
This blog post describes how to create permutations, repetition is NOT allowed. Permutations are items arranged in a given order meaning the order is important.
Examples of permutations are phone numbers, if you enter the digits in the wrong order you might phone someone else, however, phone numbers may have digits repeated and in that case repetition is allowed.
The image above demonstrates how to create permutations of a given number of items and repetition is not allowed, using a user defined function. The numbers are not repeated row-wise.
How to add the User defined Function to your workbook
- Copy the user defined function below
- Press Alt-F11 to open the Visual Basic editor
- Press with left mouse button on Module on the Insert menu
- Paste to code module
- Exit visual basic editor and go back to Excel
VBA code
Function ListPermut(num As Integer)
'Permutations without repetition
Dim c As Long, r As Long, p As Long
Dim rng() As Long, temp As Long, i As Long
Dim temp1 As Long, y() As Long, d As Long
p = WorksheetFunction.Permut(num, num)
' Create array
ReDim rng(1 To p, 1 To num)
'Create first row in array (1, 2, 3, ...)
For c = 1 To num
rng(1, c) = c
Next c
For r = 2 To p
' 1. Find the first smaller number rng(r-1, c-1)<rng(r-1,c)
For c = num To 1 Step -1
If rng(r - 1, c - 1) < rng(r - 1, c) Then
temp = c - 1
Exit For
End If
Next c
' Copy values from previous row
For c = num To 1 Step -1
rng(r, c) = rng(r - 1, c)
Next c
' 2. Find a larger number than rng(r-1, temp)as far to the right as possible
For c = num To 1 Step -1
If rng(r - 1, c) > rng(r - 1, temp) Then
temp1 = rng(r - 1, temp)
rng(r, temp) = rng(r - 1, c)
rng(r, c) = temp1
ReDim y(num - temp)
i = 0
For d = temp + 1 To num
y(i) = rng(r, d)
i = i + 1
Next d
i = 0
For d = num To temp + 1 Step -1
rng(r, d) = y(i)
i = i + 1
Next d
Exit For
End If
Next c
Next r
ListPermut = rng
End Function
How to enter the user defined function
- Select cell range B3:E26, see top image above.
- Type =ListPermut(4).
- Enter the user defined function as an array formula.
- Press and hold CTRL + SHIFT simultaneously.
- Now press Enter once.
- Release all keys.
The formula bar now shows the formula with a beginning and ending curly bracket telling you that you entered the formula successfully. Don't enter the curly brackets yourself.
Permutations category
Excelxor is such a great website for inspiration, I am really impressed by this post Which numbers add up to […]
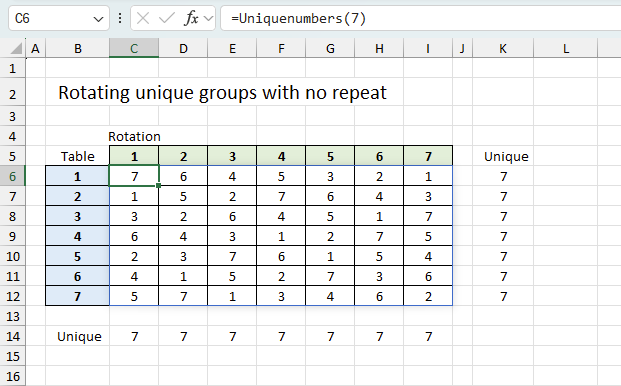
This article demonstrates ways to create unique groups with no repeat. The first example shows a formula that returns random […]
Excel categories
28 Responses to “How to create permutations”
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.

Thank you for your guide.
After follow the instructions shown and still couldn't get what i want. I am very much appreciate if you could guide me to solve my matter. My problem is:
Explanation 1 (Permutations):
Maximum Number Allowed is 4 digit and the number is from 0 to 9.
After fill in the number i want it to automotic permutate the numbers and list in details, example if i key in 1234 and the list will be:
1234, 1243, 1423, 4123, 1324, 1342, 1432, 4132, 3124, 3142, 3412, 4312, 2134, 2143, 2413, 4213, 2314, 2341, 2431, 4231, 3214, 3241, 3421, 4321.
Explanation 2 (Combinations):
Maximum Number Allowed is 10 digit and the number is from 0 to 9.
After fill in the number i want it to automotic combine the numbers and list in details, example if i key in 01234567 and the list will be:
0012, 0112, 0122, 0013, 0113, 0133, 0014, 0114, 0144, 0015, 0115, 0155, 0016, 0116, 0166, 0017, 0117, 0177, 0023, 0223, 0233, 0024, 0224, 0244, 0025, 0225, 0255, 0026, 0226, 0266, 0027, 0227, 0277, 0034, 0334, 0344, 0035, 0335, 0355, 0036, 0336, 0366, 0037, 0337, 0377, 0045, 0445, 0455, 0046, 0446, 0466, 0047, 0447, 0477, 0056, 0556, 0566, 0057, 0557, 0577, 0067, 0667, 0677, 1123, 1223, 1233, 1124, 1224, 1244, 1125, 1225, 1255, 1126, 1226, 1266, 1127, 1227, 1277, 1134, 1334, 1344, 1135, 1335, 1355, 1136, 1336, 1366, 1137, 1337, 1377, 1145, 1445, 1455, 1146, 1446, 1466, 1147, 1447, 1477, 1156, 1556, 1566, 1157, 1557, 1577, 1167, 1667, 1677, 2234, 2334, 2344, 2235, 2335, 2355, 2236, 2336, 2366, 2237, 2337, 2377, 2245, 2445, 2455, 2246, 2446, 2466, 2247, 2447, 2477, 2256, 2556, 2566, 2257, 2557, 2577, 2267, 2667, 2677, 3345, 3445, 3455, 3346, 3446, 3466, 3347, 3447, 3477, 3356, 3556, 3566, 3357, 3557, 3577, 3367, 3667, 3677, 4456, 4556, 4566, 4457, 4557, 4577, 4467, 4667, 4677, 5567, 5667, 5677.
And will have the options of Non-repeating
- One-repeating 1123
- Dual-doubles 1122
- One-tripled 1112
- Quadruples 1111
Thank you in advance and very much appreciated.
- Non-repeating 1234
- One-repeating 1123
- Dual-doubles 1122
- One-tripled 1112
- Quadruples 1111
Thank you...
Can you help me make a permutation list for 6 slots, with a +1 or -1 value. There should be a total of 64 combinations.
hi,
i'm trying to use this function. I can generate only permutations only up to 8 as function argument, does it has a limit?
thanks in advance
Andrea
andrea,
Yes, there is a limit to the vba array.
Thank-you for your Combinations formula -- Is there a way to adapt that, or use another function to distribute the resulting combinations "more equitably" over "xx" rows (of dates)? So what am I trying to accomplish? There are six tennis players(players A, B, C, D, E, and F) that share a 15 week contract(actually it's a 32 week contract) to play doubles tennis. I want to set up a schedule to distribute the resulting 15 combinations over a 15 week period that distributes evenly "when" the players play. Using the Combinations function, Player A, "plays" for the first 10 weeks, then is "off" for the next 5 weeks; Player B plays the first six weeks, and then is off for 4 weeks, then plays 4 weeks, then is off the last week; etc. Is there a way to distribute the resulting Combinations such that no player is "off" for more than one or two weeks at a time?
Any thoughts are appreciated.
Is there a way where i can predict all possible outcomes in excel in the below example.
Total games are 13 (ABCDEFGHIJKLM).Possible outcomes are win(home team),draw or win(Away team) represented by 1,X or 2 respectively.Outcomes should be in the below formats
111111111111X
11111111111XX
2222222X22221
222222222222X
Noel,
read this post:
https://www.get-digital-help.com/list-permutations-with-repetition-and-how-many-to-choose-from/
[…] Noel asks: […]
i am trying / looking for a way to write in-excel 2007, 20 numbers out of 1 to 45 like Australian lotto ,there is a site that you probaly know...will give 4 out of 4 numbers while seleecting up to 12 picked.is the a way I can show 45 numbers ie 1 to 45, then use hlookup, and get it to show the cells for the first 6 out of the 45, and so on..
thanks Bert
bert
Can you explain in greater detail?
looks like there's a syntax error with the line starting If rng(r - 1, c - 1) < rng(r - 1, c) Then..... unable to execute the code
Thanks for making your code accessible to everyone. Super helpful!
Kayla
Thank you for telling me, I hope it works now.
In case it is not working, there is a file you can try out.
Hi Oscar,
Can you give a file that i can try out for this code?
sir i have f1,f2,f3,w1,w2,w3,g1,g2,g3,r1,r2,r3
i want to make max possible combination using one of f,one of w,one of g,one of r
how will i combine and pl display it
thanks eg f1,w1,g1,r1
f2,w1,g1,r1
can i get excel for 16 digit, possible permutations with out repetition of number?
Thank you. One more question on this code. I need 3 out 5 unique permutations (e.g. 3 buttons out total 5 are selected). your code allows to list possible permutations for a given number, but not for any selection of numbers out of given numbers).
Let say, I have 5 buttons (A, B, C, D & E) and select 3 unique buttons so 60 total unique combinations are available. Not sure how to modify your code to list this in Excel.
Hi Oscar, this works great for up to 8 digits, for example =ListPermut("12345678",8) generates the correct 40,320 permutations. However for 9 digits with =ListPermut("123456789",9) it stops generating after 35,200 permutations however the correct count should be 362,880. I don't see anything in the VBA code that should cause it to stop early. Any ideas or fixes???? Thanks!
What is the code for the police example?
Elizabeth Watson,
There is a UDF found here: https://www.get-digital-help.com/excel-udf-list-permutations-without-repetition/
Dear Oscar,
Thanks for generator of this permutation.
All the list of permutation are list in the array of column. What if I want it list in the array of row instead? What part should I edit in your module code?
with regards,
hi,
can you modfied this macro for producing numbers
when order isn't important ?
like 5 out 6 of 1-2-3-4-5-6
total combinations = 6
{1,2,3,4,5} {1,2,3,4,6} {1,2,3,5,6} {1,2,4,5,6} {1,3,4,5,6} {2,3,4,5,6}
me,
there is an Excel 365 formula here: List combinations
oscar,
i'm with excel 21
don't have 365
but thanks
me,
read this: Return all combinations
hi oscar, didn't manage with it, get a an answer in another website
thanks anyway
Hello Oscar,
Thanks for the nice and informative website. I have extensively used formulas and methods described in this website for personal use.
I am trying to execute display of permutations from the given list:
Reagent 1 2 3 4
Lots
1 R1-1 R2-1 R3-1 R4-1
2 R2-2 R3-2 R4-2
3 R2-3
4 R2-4
I want to display combinations like this below:
R1-1 R1-1 R1-2 R1-2
R3-1 R3-2 R3-1 R3-2
R4-1 R4-2 R4-1 R4-2 R4-1 R4-2 R4-1 R4-2
R2-1 1 5 9 13 17 21 25 29
R2-2 2 6 10 14 18 22 26 30
R2-3 3 7 11 15 19 23 27 31
R2-4 4 8 12 16 20 24 28 32
Above example shows 32 permutations. I am working with 13 different reagents and may have lots upto 12. However, only some reagents will be subject to permutations such that total permutation does not exceed 96 nos.
The possible combinations in terms of Reagents x lots.
considering only two reagents under study can be 12 lots of Reagents-1 x 8 lots of Reagents-2 will have 96 combinations; similarly
considering all 13 reagents under study can be 7 lots of each Reagent can give max 1 combination.
I tried my level best to make you understand my problem.
Your help is highly appreciated.
Best Regards,
Shailesh
Shailesh
Can you provide an image of your data?
Perhaps this is helpful?
Create permutations using a formula